0.999･･･=1

●　小数を２進法で　●

　さて、今回は小数のお勉強をしましょう。

 　えっ、小数ぐらい知ってるって？
　０．９９９・・・＝１　だって知ってるよって？

　（知らない人は、このホームページの
　＜Ｑ＆Ａ＞の「１と０．９９９・・・どちらが大きい」を読んでね。
　それから　＜お勉強＞の「１０００−１」をまだ読んでいない人は、
　そちらを先にみてね。）

　まだまだ、続きがあるのです。

　さて、　０．９９９　をもう一度ふりかえってみましょう。

　　　　　０．９９９　は　

                                     １　
　　　　　　　^{０．１　つまり}　 １０　　^{を　９つ　と}

                                     　 １　
　　　　　　　^{０．０１　つまり}　 １００　^{を　９つ　と}

                                        　 １　
　　　　　　　^{０．００１　つまり}　 １０００　^{を　９つ　を}

　あわせた数です。すなわち、

　　　　　　　　　　　_{９　　　　　　　　９　　　　　　　　　９}
　　　^{０．９９９　＝}　１０　　　^＋　　１００　　　^＋　　１０００

　では、２進法で　０．１１１　といったらどんな数でしょうか。
（これを　（０．１１１）_２とかくことにします。）

　それには、１０　を　２　でおきかえます。

　　　　　（０．１１１）_２は

　　　　　　　　　　　１　
　　　　　　　　　　　２　　^{を　１つ　と}

　　　　　　　　　　　１　
　　　　　　　　　　　４　　^{を　１つ　と}

　　　　　　　　　　　１　
　　　　　　　　　　　８　　^{を　１つ　を}

　あわせた数です。つまり、

　　　　　　　　　　　　　　 _{１　　　　　　　１　　　　　　　　１}
　　　　^{（０．１１１）}_２^＝　 ２　　　^＋　　　４　　　^＋　　　８

　これは１０進法ではどんな数か、続けて計算しておきましょう。

　　　　　　　　　　　　　   _{４　　　　　　　２　　　　　　　　１}
　　　　　　　　　　　　^＝ 　 ８　　　^＋　　　８　　　^＋　　　８

　　　　　　　　　　　　　　_７
^＝ 　 ８　

　　　　　　　　　　　　＝　０．８７５

　２進法で　（０．１１１）_２は　１０進法で　０．８７５　です。

　さて、いよいよこんなことを考えてみましょう。
　１０進法で次のことは、２進法ではどんなことかな？

　　　　　０．９９９・・・＝１

　くりかえします。　
　これの２進法版はどうなるでしょう？

　「１０００−１」で、こんなことをやりました。
　１０進法で　あと　１　で　１０　になる数は　９　です。
　そして、２進法で　あと　１　で　２　になる数は　１　でした。
　ですから、こんなことになります。

　　　　　（０．１１１・・・）_２＝１

　これは１０進法になおすと、次のようになります。

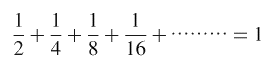
●　２進法から１０進法へ（整数）　●

　このさい、２進数についてもっとお勉強してみましょう。

　まずは、２進法で表された数を１０進法で表すことからやります。

　こんなふうに考えましょう。

　２進法のコンピュータ社会のお金を、１０進法の人間社会のお金に、
両替（りょうがえ）するのです。

　ためしに、（１０１０１）_２　円　を両替してみます。
　まず、コンピュータ社会で　全部１円玉にくずしてしまいます。

　　　　　１円玉　が　１個　と
　　　　　２円玉　が　０個　と
　　　　　４円玉　が　１個　と
　　　　　８円玉　が　０個　と
　　　　１６円玉　が　１個　とでは　　全部　１円玉　にすると　２１個　です。

　まず、このコンピュータ社会の　１円玉　２１個　を
　人間社会の　１円玉　２１個　に両替します。
　（もちろんどちらの１円玉も　数学社会　では　同じ　１　です。）

　この　１円玉　２１個　を　今度は人間社会で大きなお金にかえていきます。
　１円玉　２１個　のうち　２０個　を　１０円玉　２個　にかえると

　　　　　１円玉　が　１個　と
　　　　１０円玉　が　２個　になり　もちろん　２１円　です。

　コンピュータ社会の　（１０１０１）_２　円は、人間社会の　（２１）₁₀　円　です。

　まとめてみましょう。

　　　１円　　　　　　　　　　　　　　　　　　　　（　このことを　２⁰　）
　　　２円　　　　　　　　　　　　　　　　　　　　（　このことを　２¹　）
　　　４円　　は　２×２　　　　　　　　　　　　　　このことを　２²　
　　　８円　　は　２×２×２　　　　　　　　　　　 このことを　２³　
　　１６円　　は　２×２×２×２　　　　　　　　　このことを　２⁴　

　そして、１０進法の１の位、１０の位、１００の位　などは、
２進法では次のようなことです。

　　（１０１０１）_２で　１　のところは　　１の位　（２⁰の位）
　　　　　　　　　　０　のところは　　２の位　（２¹の位）
　 　　　　　　　　　　　　　１　のところは　　４の位　（２²の位）
　　　　　　　　　　０　のところは　　８の位　（２³の位）
　　　　　　　　　　１　のところは　１６の位　（２⁴の位）

　この書き方で、もう一度計算しておきましょう。

　（１０１０１）_２＝１×２⁴　＋　０×２³　＋　１×２²　＋　０×２　＋　１×１
　　　　　　＝１×１６＋　０×８　＋　１×４　＋　０×２　＋　１×１
　　　　　　＝　１６　＋　　０　　＋　　４　　＋　　０　　＋　　１
　　　　　　＝　２１

●　１０進法から２進法へ（整数）　●

　次に、１０進法で表された数を２進法で表してみましょう。

　また、こんなふうに考えます。

　１０進法の人間社会のお金を、２進法のコンピュータ社会のお金に、
両替（りょうがえ）するのです。

　ためしに、（２１）₁₀　円　を両替してみます。
　まず、人間社会で　全部１円玉にくずしてしまいます。

　　　　　１円玉　が　１個　と
　　　　１０円玉　が　２個　とでは　　全部　１円玉　にすると　２１個　です。

　まず、この人間社会の　１円玉　２１個　を
　コンピュータ社会の　１円玉　２１個　に両替します。
　（もちろんどちらの１円玉も　数学社会　では　同じ　１　です。）

　この　１円玉　２１個　を　今度はコンピュータ社会で大きなお金にかえていくのです。

　さあ、銀行屋さん（両替屋さん）ごっこです！

●　まず、１円玉　２１個　を　２円玉　にかえます。
 　　１円玉　２個　につき　２円玉　１個　にかえます。

　　　　　２１÷２＝１０　あまり　１　　これを　　２　）　２１　
 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　１０　・・・１

　１円玉　２０個　は　２円玉　１０個　にかえられます。
　でも　あまった　１個　は　１円玉のままです。
　ですから、１円玉　は　１個　とわかります。

●　つぎに、２円玉　１０個　を　４円玉　にかえます。
 　　２円玉　２個　につき　４円玉　１個　にかえます。

　　　　　１０÷２＝５　あまり　０　　これを　　２　）　１０　
 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　５　・・・０

　２円玉　１０個　は　４円玉　５個　にかえられます。
　そして、２円玉　は　あまりませんでした。
　ですから、２円玉　は　０個　とわかります。

●　つぎに、４円玉　５個　を　８円玉　にかえます。
 　　４円玉　２個　につき　８円玉　１個　にかえます。

　　　　　５÷２＝２　あまり　１　　これを　　２　）　　５　
 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２　・・・１

　４円玉　４個　は　８円玉　２個　にかえられます。
　でも　あまった　１個　は　４円玉のままです。
　ですから、４円玉　は　１個　とわかります。

●　つぎに、８円玉　２個　を　１６円玉　にかえます。
 　　８円玉　２個　につき　１６円玉　１個　にかえます。

　　　　　２÷２＝１　あまり　０　　これを　　２　）　　２　
 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　１　・・・０

　８円玉　２個　は　１６円玉　１個　にかえられます。
　そして、８円玉　は　あまりませんでした。
　ですから、８円玉　は　０個　とわかりました。

●　けっきょく、　１円玉　１個
　 　　　　　　　 　２円玉　０個
　　 　　　　　 　　４円玉　１個
　　　 　　　　　 　８円玉　０個
　　　　 　　　 　１６円玉　１個
　とかえられました。

●　いままでの計算は、次のように続けてやっていきます。

　　　　　　２　）　２１　
  　　　　　２　）　１０　・・・　１
　　　　　　２　）　　５　・・・　０
　　　　　　２　）　　２　・・・　１
　　　　　　　　　　　１　・・・　０

　人間社会の　（２１）₁₀　円は、コンピュータ社会の　（１０１０１）_２　円　です。

●　２進法から１０進法へ（小数）　●

　さて、いよいよ小数です。

　むかしは、１円　より小さいお金があったようですが、
さすがのわたしも使ったことはありません。

　でも、お金ってとってもわかりやすいので、
このさいですから、頭の中で作ってしまいましょう。

　人間社会では、次のようなお金を作ります。

　　　　　　１　
　　　　　 １０　　^{円玉　これは　１０個　で　１円　です。}

　　　　　　１　　　　　　　　　　　　　　　　　　　　１　
　　　　　１００　　^{円玉　これは　１０個　で}１０^{円　です。}

　　　　　　 １ 　　　　　　　　　　　　　　　　　　　 　１　　
　　　　　１０００　　^{円玉　これは　１０個　で}１００^{円　です。}

　同じようにして、コンピュータ社会では、次のようなお金を作ります。

　　　　　　１　
　　　　　  ２　　^{円玉　これは　２個　で　１円　です。}

　　　　　　１　　　　　　　　　　　　　　　　　　１　
　　　　　　４　　^{円玉　これは　２個　で}  ２^{円　です。}

　　　　　　 １ 　　　　　　　　　　　　　　　　 　１　　
　　　　　　 ８　　^{円玉　これは　２個　で} ４^{円　です。}

　これで、じゅんびができました。

　さっそく、２進法で表された小数を１０進法で表すことからやります。

　またまた、こんなふうに考えましょう。

　２進法のコンピュータ社会のお金を、１０進法の人間社会のお金に、
両替（りょうがえ）するのです。

　ためしに、（０．１０１）_２　円　を両替してみます。

　　　　　　　　　　　　　　 _{１　　　　　　　０　　　　　　　　１}
　　　　^{（０．１０１）}_２^＝　 ２　　　^＋　　　４　　　^＋　　　８

　　　　　　　　　　　　　　 _{４　　　　　　　０　　　　　　　　１}^＝　 ８　　　^＋　　　８　　　^＋　　　８

　　　　　　　　　　　　　　_５
^＝ 　 ８　

　　　　　　　　　　　　＝　０．６２５

　　コンピュータ社会の　（０．１０１）_２　円は、人間社会の　（０．６２５）₁₀　円　です。

●　１０進法から２進法へ（小数）　●

　いよいよ、１０進法で表された小数を２進法で表すことをやります。

　こんなふうに考えましょう。

　２進法のコンピュータ社会のお金を、１０進法の人間社会のお金に、
両替（りょうがえ）するのです。

　ためしに、（０．６２５）₁₀　円　を両替してみます。

　一見、さっきの逆をすればいいと思ってしまいます。

　　　　　　　　　　　　　　　_６２５
　　　　^{（０．６２５）}₁₀^＝ 　 １０００　

　　　　　　　　　　　　　　_５
^＝ 　 ８

　　　　　　　　　　　　　　_{４＋０＋１}
^＝ 　 　　８

　　　　　　　　　　　　　　_{４　　　　　　　０　　　　　　　　１}^＝　 ８　　　^＋　　　８　　　^＋　　　８

　　　　　　　　　　　　　　 _{１　　　　　　　０　　　　　　　　１}^＝　　 ２　　　^＋　　　４　　　^＋　　　８

　一見めでたく、人間社会の　（０．６２５）₁₀　円は、
コンピュータ社会の　（０．１０１）_２　円　です、となりそうですね。

　ところが、そうはとんやがおろさないのです。

　たとえば、（０．２）₁₀　円　を両替してみましよう。

　　　　　　　　　　　　_２
　　　　^{（０．２）}₁₀^＝ 　 １０　

　　　　　　　　　　　　_１
^＝ 　 ５

　にっちもさっちもいかなくなりますね。

　そこで、気分もあらたに　（０．６２５）₁₀　円　の両替からもう一度やってみます。

　１０進数 の場合は

　　　　　１円玉　は　何枚？
　　　　１０円玉　は　何枚？
　　　１００円玉　は　何枚？

と数えねばならずめんどうでしたが、２進数の場合はどのお札（玉）も

　　　０枚　それとも　１枚

と数えるだけですからかんたんです。

　さあ、あるかな（０枚）　それとも　ないかな（１枚）？

　　　　　　　　　　　　　　　　　　１　
　^{●まず　０．６２５円　で}　　  ２　　^{円玉　はありそうです。}

　　１　
　  ２　　^{円玉　　は　２個　で　１円　でしたが、}０．６２５円　は　２倍　して　１円　をオーバーするからです。

　　　　　０．６２５　×　２　＝　１．２５

　　　　　　　　　　　　　　　 ＝　１＋０．２５

　　　　　　　　　　　　　　　　　　　　１　
　^{ここで、１＋０．２５　の　１　は}  ２　　^{円玉　の枚数です。}

　０．２５　は　のこりのお金の２倍です。

　　　　　　　　　　　　　　　　　　　１　
　^{●次に　のこりのお金に}　　   ４　　^{円玉　はなさそうです。}

　　１　
　  ４　　^{円玉　　は　４個　で　１円　でしたが、}０．２５円　は　すでに　２倍　してありますから
もう　２倍してみますが　　それでも　１円　にたりないからです。

　　　　　０．２５　×　２　＝　０．５

　　　　　　　　　　　　　　 ＝　０＋０．５

　　　　　　　　　　　　　　　　　　　　１　
　^{ここで、０＋０．５　の　０　は}  　４　　^{円玉　の枚数です。}

　０．５　は　のこりのお金の４倍です。

　　　　　　　　　　　　　　　　　　　１　
　^{●次に　のこりのお金に}　　   ８　　^{円玉　はありそうです。}

　　１　
　  ８　　^{円玉　　は　８個　で　１円　でしたが、}０．５円　は　すでに　４倍　してありますから
もう　２倍してみると　　ちょうど　１円　になります。

　　　　　０．５　×　２　＝　１

　　　　　　　　　　　　１　
　^{ここで、　１　は}  　８　　^{円玉　の枚数です。}

　これで、もうお金はのこっていず、全部両替されました。

　●　もう一度ふりかえってみましょう。

　人間社会の　（０．６２５）₁₀　円は、コンピュータ社会の　（０．１０１）_２　円　です。

　さて、問題の　（０．２）₁₀　円　を両替してみましよう。

　　　　　　　　　　　　　　　　１　
　^{●まず　０．２円　で}　　  ２　　^{円玉　はなさそうです。}

　　１　
　  ２　　^{円玉　　は　２個　で　１円　でしたが、}０．２円　は　２倍　しても　１円　にたりないからです。

　　　　　０．２　×　２　＝　０．４

　　　　　　　　　　　　　 ＝　０＋０．４

　　　　　　　　　　　　　　　　　　　１　
　^{ここで、０＋０．４　の　０　は}  ２　　^{円玉　の枚数です。}

　０．４　は　のこりのお金の２倍です。

　　　　　　　　　　　　　　　　　　　１　
　^{●次に　のこりのお金に}　　   ４　　^{円玉　もやっぱりなさそうです。}

　　１　
　  ４　　^{円玉　　は　４個　で　１円　でしたが、}０．４円　は　すでに　２倍　してありますから
もう　２倍してみますが　　それでも　１円　にたりないからです。

　　　　　０．４　×　２　＝　０．８

　　　　　　　　　　　　　 ＝　０＋０．８

　　　　　　　　　　　　　　　　　　　　１　
　^{ここで、０＋０．８　の　０　は}  　４　　^{円玉　の枚数です。}

　０．８　は　のこりのお金の４倍です。

　　　　　　　　　　　　　　　　　　　１　
　^{●次に　のこりのお金に}　　   ８　　^{円玉　はありそうです。}

　　１　
　  ８　　^{円玉　　は　８個　で　１円　でしたが、}０．８円　は　すでに　４倍　してありますから
もう　２倍してみると　　今度は　１円　をオーバーします。

　　　　　０．８　×　２　＝　１、６

　　　　　　　　　　　 　　＝　１＋０．６

　　　　　　　　　　　　１　
　^{ここで、　１　は}  　８　　^{円玉　の枚数です。}

　　　　　　　　　　　　　　　　　　　１　
　^{●次に　のこりのお金に}　　  １６　　^{円玉　はありそうです。}

　　１　
　 １６　　^{円玉　　は　１６個　で　１円　でしたが、}０．６円　は　すでに　８倍　してありますから
もう　２倍してみると　　今度も　１円　をオーバーします。

　　　　　０．６　×　２　＝　１、２

　　　　　　　　　　　 　　＝　１＋０．２

　　　　　　　　　　　　１　
　^{ここで、　１　は}  　１６　　^{円玉　の枚数です。}

　●さて、のこりのお金の１６倍は　最初の　０．２　です。
　　ここから、おなじことのくりかえしになります。

　●　もう一度ふりかえってみましょう。

　　つまり、人間社会の　（０．２）₁₀　円は、
コンピュータ社会の　（０．００１１００１１００１１・・・）_２　円　になります。

●　循環小数　●

　もしかしたら、

　　（０．２）₁₀　＝　（０．００１１００１１００１１・・・）_２

と、（２進数版）循環小数（じゅんかんしょうすう）になったことを、
ぐうぜんと思っていませんか。

　では、２進数でわり算をやってみましょう。

　　　　　　　　　　　　　　　_６２５
　　　　^{（０．６２５）}₁₀^＝ 　 １０００　

　　　　　　　　　　　　　　_５
^＝ 　 ８

　　　　　　　　　　　　　　_{（１０１）２}
^＝ 　 （１０００）_２

　ここから、わり算をします。

　　　　　　　　　　　　　　０．１０１
　　　　　１０００　）　１０１
　　　　　　　　　　　　１０００
　　　　　　　　　　　　　　１０００
　　　　　　　　　　　　　　１０００
　　　　　　　　　　　　　　　　　０

　したがって　（０．６２５）₁₀　＝　（０．１０１）_２

　さて、問題の循環小数になる方をやりましょう。

　　　　　　　　　　　　　　_２
　　　　　　^{（０．２）}₁₀^＝ 　 １０　

　　　　　　　　　　　　　　_１
^＝ 　 ５

　　　　　　　　　　　　　　_（１）２
^＝ 　（１０１）_２

　これも、ここからわり算をします。

　　　　　　　　　　　　０．００１１
　　　　　　１０１　）　１．００００
　　　　　　　　　　　　　　１０１
　　　　　　　　　　　　　　　１１０
　　　　　　　　　　　　　　　１０１
　　　　　　　　　　　　　　　　　１

　ここで　１÷１０１　になりましたから、ここから同じことのくりかえしです。

　数を２進法であらわしても、あまりは割る数より小さいのですから
５（１０１）　より小さい数の、　０（０）、１（１）、２（１０）、３（１１）、４（１００）
のどれかになります。
　それでいつかは同じあまりがでてきて、そこから同じことのくりかえしとなります。
　こういうわけで、循環するのです。

　したがって　（０．２）₁₀　＝　（０．００１１００１１００１１・・・）_２

HOME（もどる）

掲載内容の無断転載、転用、編集を禁じます。(c) 小林吹代
All Rights Reserved, （c）kobayashi fukiyo , 2001