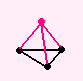4次元
● 超立方体 ●
下の図を見てください。
あらっ、ステキなモザイクもよう!
もしかしたら、ダイヤモンドのカット図かしら・・・。
じつは、これは4次元の立方体(を平面にかいたもの)なのです。
(色をつけない方が、それらしく見えますよ。)
4次元の立方体は、
超立方体(ちょうりっぽうたい)とか正8胞体(ほうたい)と
いわれています。
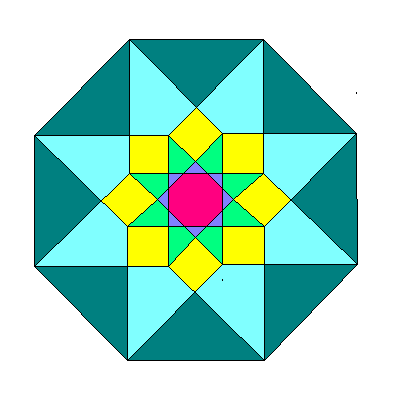
でも、いきなりこんなものが4次元の立方体といわれても
・・・こまってしまいますね。
そこで、話をいったん0次元にもどしてから、
じゅんに次元を上げて、みていくことにしましょう。
● 次元 ●
4次元というと、なんとなくミステリアス。
まるで、SFみたい・・・。
そんな気持ちにザバーッと水をぶっかけるような話に
ならないといいのですが・・・。
< 0次元 >
まずは、0次元です。
点です。
●
何もいうことはありません。
< 1次元 >
次は、1次元です。
直線です。
1次元の立方体って・・・?
0次元の点を、スーッと(べつの次元に1だけ)もちあげると、
線分ができます。
![]()
これを、1次元の立方体(?)ということにしましょう。
< 2次元 >
次は、2次元です。
平面です。
2次元の立方体って・・・?
1次元の線分を、スーッと(べつの次元に1だけ)もちあげると、
正方形ができます。

これを、2次元の立方体(じつは正方形)ということにしましょう。
< 3次元 >
次は、3次元です。
空間です。
3次元の立方体って・・・?
2次元の正方形を、スーッと(べつの次元に1だけ)もちあげると、
立方体ができます。
これは、3次元の立方体(これが本当の立方体)です。
< 4次元 >
次は、いよいよ4次元です。
4次元空間です。
4次元の立方体って・・・?
3次元の立方体を、スーッと(べつの次元に1だけ)もちあげると、
(4次元なんて、どこにもちあげていいのやら・・・)
4次元の立方体(超立方体)ができるはずです。
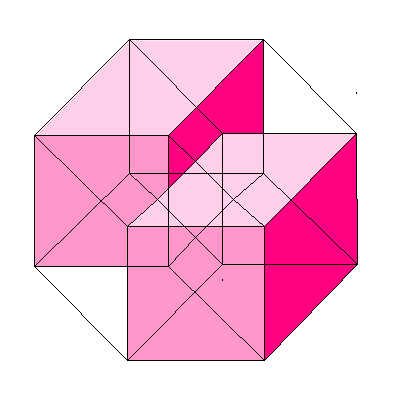
これを、4次元の立方体、つまり超立方体ということにしましょう。
(色のつけ方ひとつで、ずいぶんとちがって見えるものですね。
ほかに、いくつ立方体が見えますか?
ちゃんと8個みえますか?
正8胞体っていうからには8個なくっちゃ〜ねっ!)
● 単体 ●
さて、なにごとでもそうですが、
いきなりむずかしいことをやっても、うまくいきません。
頂点や辺や面の個数をかぞえるのだってそうです。
まずは、もっとかんたんな場合からやってみましょう。
立方体より、もっと頂点や辺や面の個数が少ないもの・・・
そうです!
正方形でなくって・・・三角形!
立方体でなくって・・・四面体!
さあ、かぞえましょう!かぞえましょう!!
< 0次元 >
まずは、0次元です。
点です。
0次元では、正方形も三角形もあったものではありませんね。
|
|
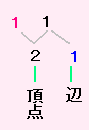
頂点があらわれる。 | 1 | 頂 点 |
< 1次元 >
次は、1次元です。
直線です。
1次元の三角形って・・・?
0次元の点をつまんで、(べつの次元に)もちあげると、
線分ができます。
1次元でも、やっぱり正方形とおなじです。
|
|
新しい頂点が1つくわわり 頂点の個数は 1+1=2 辺があらわれる。 |
|
< 2次元 >
次は、2次元です。
平面です。
2次元の三角形って・・・ふつうの三角形ですよね。
1次元の線分をつまんで、ゴムひものように(べつの次元に)もちあげると、
三角形ができます。
|
|
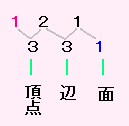
新しい頂点が1つくわわり 頂点の個数は 2+1=3 辺の個数はもとの頂点とむすんだだけふえ 面があらわれる。 |
 |
< 3次元 >
次は、3次元です。
空間です。
3次元の三角形って・・・四面体ですよね。
2次元の三角形をつまんで、ゴムまくのように(べつの次元に)もちあげると、
四面体ができます。
|
|
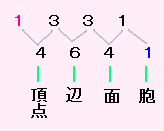
新しい頂点が1つくわわり 頂点の個数は 3+1=4 辺の個数はもとの頂点とむすんだだけふえ 面はもとの辺の個数だけふえ 胞があらわれる。 |
 |
ちなみに胞(ほう)というのは、四面体のなかみ(?)です。
< 4次元 >
次は、いよいよ4次元です。
4次元空間です。
4次元の四面体って・・・?
3次元の四面体をつまんで、アメーバのように(べつの次元に)もちあげると、
4次元の超四面体(5胞体)ができるはずです。
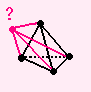 |
新しい頂点が1つくわわり 頂点の個数は 4+1=5 あとも同じように(?) 面の個数はもとの辺の個数だけふえ 胞の個数はもとの面の個数だけふえ ?があらわれる。 |
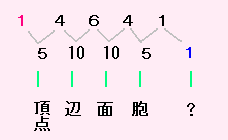 |
この4次元の超四面体は、胞が5個なので5胞体とよばれています。
4次元であらわれる ? は何とよばれているのかって?
(知っている人はメールください!)
まずこれで、(4次元の)5胞体の頂点・辺・面・胞の個数がわかりました。
じつは、3次元では正多面体があったように、
4次元では正多胞体というのがあります。
そのなかに、正5胞体というのがちゃんとありまして、
正5胞体 ・・・ 頂点(5個)、辺(10個)、面(10個)、胞(5個)
となっています。
● パスカルの三角形 ●
この表をみてください。
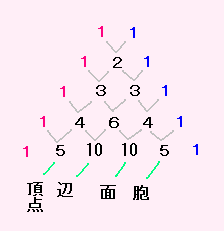
あら、どこかで見たような・・・
そうです!このホームページでも、一度やりましたね。
パスカルの三角形です。
そこでは、パスカルの三角形の数は
2項定理で出てくる数だよ・・・ってこともやりました。
こんなことでしたね。
(a+b)1 = 1a + 1b
(a+b)2 = 1a2 + 2ab + 1b2
(a+b)3 = 1a3 + 3a2b + 3ab2 + 1b3
(a+b)4 = 1a4 + 4a3b + 6a2b2 + 4ab3 + 1b4
(a+b)5 = 1a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + 1b5
ここで、a=b=1にすると、
21 = 1+1
22 = 1+2+1
23 = 1+3+3+1
24 = 1+4+6+4+1
25 = 1+5+10+10+5+1
のようになります。
これは、0次元、1次元、2次元、3次元、4次元の
三角形や四面体や超四面体のようなものの
頂点、辺、面、胞の個数と1と1をあわせると2の何乗かになるって式ですね。
でも、こんな式はぜんぜん有名ではありません。
どうして有名にならないかって?
三角形でなくって四角形にしたら・・・
四面体でなくって立方体にしたら・・・
頂点も辺も面も胞も、もっともっと多くなってしまうからです。
三角形や四面体だけの式なんて、有名になりっこありません。
ところがです。
2項定理で、a=1、b=−1にするとどうでしょう。
0 = 1−1
0 = 1−2+1
0 = 1−3+3−1
0 = 1−4+6−4+1
0 = 1−5+10−10+5−1
これは、1次元、2次元、3次元、4次元の
三角形や四面体や超四面体のようなものの
頂点、辺、面、胞の数と1と1をたしたりひいたりすると0になるって式ですね。
こっちは有名です。
どうして有名になったかって?
これを、こんなふうに書きなおしてみるのです。
| 0次元 なら 0=1−1 1次元 なら 0=1−(頂点)+1 2次元 なら 0=1−(頂点)+(辺)−1 3次元 なら 0=1−(頂点)+(辺)−(面)+1 4次元 なら 0=1−(頂点)+(辺)−(面)+(胞)−1 |
さらに、この式をてきとうになおすと、次のようになります。
| 0次元 なら どれも同じで、何もいうことなし! 1次元 なら どれも同じで、(頂点)=2 2次元 なら (頂点)=(辺) 3次元 なら (頂点)−(辺)+(面)=2 4次元 なら (頂点)−(辺)+(面)−(胞)=0 |
さて、こっちの方は、どうして有名になれたかってことでしたね。
もちろん、それは
三角形でなくって四角形にしたら・・・
四面体でなくって立方体にしたら・・・
頂点も辺も面も胞も、もっともっと多くなってしまうけれど、
今度はひき算もあるから・・・
プラス・マイナス 0 となって、うまくいくからなんですね。
もちろん、「うきわ」のように「あな」があいているものはダメですよ。
さて、本当にプラス・マイナス 0 になるかというお話は、
(いつもながら)また今度ということにしましょう。
● オイラーの多面体定理 ●
有名なのは、とくに3次元の場合です。
(アインシュタインが何と言おうと、この世は3次元だから(?)
4次元の<じく>を時間にとるなんて・・・)
3次元 なら (頂点)−(辺)+(面)=2 でしたね。
これには、名前までついているのです。
発見者にちなんで、オイラーの多面体定理って言うのです。
さあ〜て、いよいよ前回の「正多面体」でやりのこしたことをやりましょう。
こんなことでした。
![]()
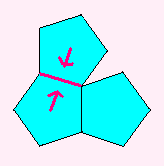
正12面体で、1つの頂点のまわりに、
正5角形を3枚使って作っていったら何枚でできるか・・・
ということは、ちょっとおいておいて、
とりあえず12枚でできたということから話をはじめてしまいました。
そこで今回は、何枚でできるかってところを考えるのです。
もちろん、このオイラーの多面体定理をつかってみるのです。
まず、正5角形の面の枚数を x とします。
すると、頂点の個数は 5x ではなくって、5x/3 です。
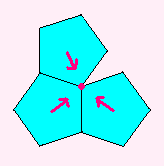
また、辺の個数は 5x ではなくって、5x/2 です。
これを、 (頂点)−(辺)+(面)=2 に入れます。
5x 5x
---- − ---- + x = 2
3 2
10x − 15x + 6x = 12
x = 12
ということで、できるとしたら12枚ってことで、
けっきょく、12枚で作ってみるハメに・・・(?)
(あのペンタグラムは、いったい何だったの・・・)
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001