カタラン数(2)
● パスカルの三角形 ●
パスカルの三角形には、カタラン数
1 , 1 , 2 , 5 , 14 , 42 , ・・・
がひそんでいました。
前回は、まん中の数から、わり算してでてきましたね。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
これから、
1÷1=1
2÷2=1
6÷3=2
20÷4=5
70÷5=14
252÷6=42
というぐあいに、カタラン数
1 , 1 , 2 , 5 , 14 , 42 , ・・・
がでてきました。
(もっとも、カタラン数って、そもそも何なのだ〜
ということを、まだお話していなかったのですが、
それは、またそのうち・・・)
じつは、パスカルの三角形には、
ほかにもカタラン数がひそんでいるのです。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
さっきは、わり算をしましたが、
こんどは、ひき算をするのです。
1=1
2−1=1
6−4=2
20−15=5
70−56=14
252−210=42
ほら、カタラン数
1 , 1 , 2 , 5 , 14 , 42 , ・・・
がでてきました。
では、どうしてカタラン数がでてくるのか、
これからみていきましょう。
● 中への(1対1)対応 ●
今回も、パスカルの三角形をよこにねかせて考えましょう。
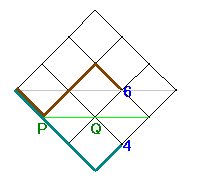
どれも、おなじようにやれますので、今回は
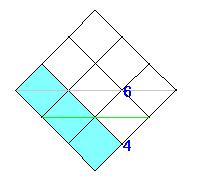
6−4=2
として出てきた 2 が、カタラン数になっていることを見てみます。
|
|
|
まず、(水色の)4通りある行き方を、
それぞれ(黄色い)6通りある行き方のうちの4通りに対応(たいおう)させます。
|
|
|
|
|
|
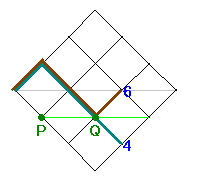
対応(たいおう)のさせ方は、
みどり色の線のところまでは同じ行き方で、
そこからさきだけ、みどり色の線について対称(たいしょう)になっているものと
対応させるのです。
そうすれば、4のところと、6のところは、
みどり色の線について対称なところにありますから、
対応させることができるのです。
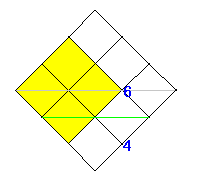
それでは、(黄色い)6通りある行き方のうちの
のこりの2通りは、どんな行き方でしょうか。
それは、みどり色の線のところまで来ない、
つまり、ず〜っと上ばかり通っていく行き方です。
前回の「カタラン数(1)」で、ついている「わりあい」として
2/2 つまり ず〜っと上 か
1/2 つまり 半分上 で 半分下 か
0/2 つまり ず〜っと下 かです。
と3つにわけた、2/2のばあいになるのです。
この3つのばあいは、どれも同じだけあって、
6÷3=2
として、でてきました。
(いまのところ)これがカタラン数というものでしたね。
ですから、6−4=2 として出てきた 2 は、
カタラン数になっているというわけです。
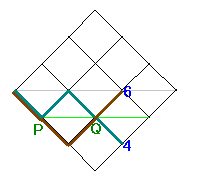
ところで、6 と 4 の 4の方は、6通りのうちの
1/2 つまり 半分上 で 半分下 か
0/2 つまり ず〜っと下 か
をあわせたものです。
ですから、もちろん
4 : 6 = 2 : 3
となっています。
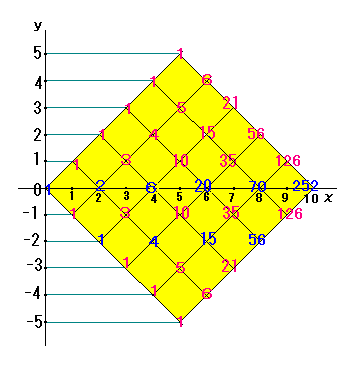
同じようにして、パスカルの三角形では、つぎのようになります。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
ここで、
1 : 2 = 1 : 2
4 : 6 = 2 : 3
15 : 20 = 3 : 4
56 : 70 = 4 : 5
210 : 252 = 5 : 6
となっています。
● パスカル風三角形 ●
今度は、このホームページの「パスカルの三角形」でやったように、
道順(みちじゅん)の個数をかぞえて、カタラン数をだしてみましょう。
(どれも同じ数だけあるのですから)
ず〜っと上を通っていく行き方をかぞえてみます。
つまり、上半分で考えます。
やり方は、(和の法則を使うだけで)
このホームページの「パスカルの三角形」でやったのと同じです。
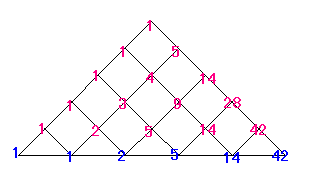
ほら、カタラン数
1 , 1 , 2 , 5 , 14 , 42 , ・・・
がでてきましたね。
この「パスカル風三角形」から、こんなことがわかります。
1= 12
1= 12
2= 12 + 12
5= 12 + 22
14= 12 + 32 + 22
42= 12 + 42 + 52
どれも同じようにしていえますので、
42= 12 + 42 + 52
で見てみましょう。
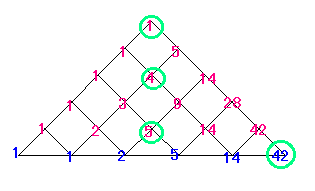
まず、42 のところに行くには
1 のところか
4 のところか
5 のところを
通らなくてはいけません。
1 のところは 1×1 通り
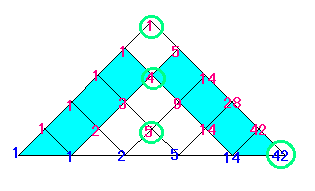
4 のところは 4×4 通り
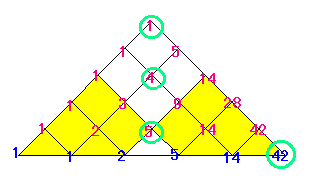
5 のところは 5×5 通り
となって、けっきょく
42= 12 + 42 + 52
となります。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001