カタラン数(3)
● カタラン数 ●
カタラン数は、このホームページでは、
道順(みちじゅん)が何通りあるかという個数でしたね。
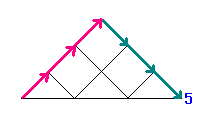
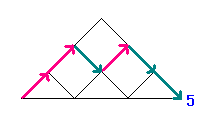
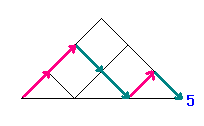
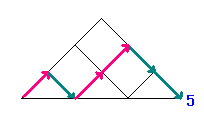
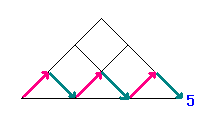
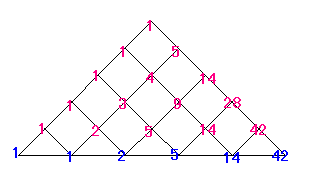
たとえば、下の図で青い数字になっているところまで
(より道しないで)いく行き方は、
1 , 1 , 2 , 5 , 14 , 42 , ・・・
です。
そして、これがカタラン数とよばれるものでした。
(ちなみに、いちばん下の青い数字をむすぶ線は道ではありませんよ!)
でも、さいしょにカタランが考えたのは、道順の個数ではなく、
こんな問題でした。
たとえば、
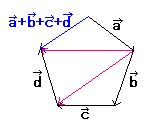
a+b+c+d
のたし算の順番(じゅんばん)を考えます。
(もちろん、a×b×c×d のように、かけ算でもいいのです。)
そうすると、つぎの 5 通りがあります。
(((a+b)+c)+d)
((a+(b+c))+d)
((a+b)+(c+d))
(a+((b+c)+d))
(a+(b+(c+d)))
えっ、いちばん外のかっこは、つけなくっていいって?
じつは、これからのお話のつごうというものがあるのです。
このように、
たし算やかけ算などの順番のつけ方が何通りあるか
といった問題を、カタランは考えたのです。
● 結合の方法 と 道順の個数 ●
さて、これから
たし算の順番のつけ方 と 道順の個数
が同じ数だけあることをみていきましょう。
同じ個数だけあるっていいたいときには・・・
そう、「1対1の対応(たいおう)」をつけてみせればいいのですね。
このホームページの「トーナメント戦」の
<森の木を数える>のところでやったようにねっ!
その前に、
(((a+b)+c)+d)
((a+(b+c))+d)
((a+b)+(c+d))
(a+((b+c)+d))
(a+(b+(c+d)))
から、いらないものをけしてしまいます。
まず、a b c d をけします。
(((+)+)+)
((+(+))+)
((+)+(+))
(+((+)+))
(+(+(+)))
これから、もとのa b c d がある形にもどす方法は
1通りですから、いらないってことで、けしてしまうのです。
(ためしに、やってみてね!)
でも、「+」は、けしてはいけません。
たとえば、
(((+)+)+)
から、「+」をけすと
( ( ( ) ) )
となりますが、これでは
(((a+b)+c)+d)
((a+(b+c))+d)
(a+((b+c)+d))
(a+(b+(c+d)))
といろいろあって、もとにもどしようがなくなります。
ところが、じつは「 )」なら、いらないのです。
(((+++
((+(++
((++(+
(+((++
(+(+(+
これから、もとのa b c d と 「 )」 がある形にもどす方法は
1通りなのです。
さて、この3つの「( 」 と 3つの「+」 のならべ方ですが、
(((+++
((+(++
((++(+
(+((++
(+(+(+
これらはどれも、とちゅうまでの「( 」の個数が、
「+」の個数より多いか同じであるものになっています。
たとえば、
((+(++
でみてみると、
( ・・・ ここまでの 「( 」は1個 、「+」は0個
(( ・・・ ここまでの 「( 」は2個 、「+」は0個
((+ ・・・ ここまでの 「( 」は2個 、「+」は1個
((+( ・・・ ここまでの 「( 」は3個 、「+」は1個
((+(+ ・・・ ここまでの 「( 」は3個 、「+」は2個
((+(++ ・・・ ここまでの 「( 」は3個 、「+」は3個
と、ちゃんとなっていますね。
このことは、道順でいうと
とちゅう1度もそんをしない、つまりず〜っと上の方にいるってことです。
もう、何に何を対応させればいいか、わかりましたね。
つぎのようになります。
|
(((+++ |
|
|
((+(++ |
|
|
((++(+ |
|
|
(+((++ |
|
|
(+(+(+ |
|
● オイラーの三角形分割問題 ●
カタランよりも先に、オイラーという数学者が
こんなことを考えました。
n角形を三角形に分ける方法は何通りあるだろうか
そして、ちゃんと答えをみつけたのです。
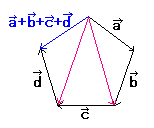
それは、5角形なら、
(((a+b)+c)+d)
((a+(b+c))+d)
((a+b)+(c+d))
(a+((b+c)+d))
(a+(b+(c+d)))
と同じ、つまり5通りあるのです。
さあ、このことをみていきましょう。
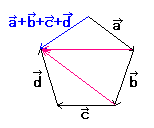
ところで、「ベクトル」って知っていますか。
中学生なら、理科の時間に「力の平行四辺形」として習っているかも。
高校生なら、数学の時間にやるはずですよ。
ここでは、ただの数の
a+b+c+d
のたし算の順番ではなく、ベクトルのたし算の順番を考えます。
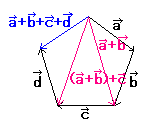
たし算をすると、対角線(たいかくせん)で三角形に分けられます。
すると、つぎのようになります。
|
(((a+b)+c)+d) |
|
|
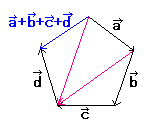
((a+(b+c))+d) |
|
|
((a+b)+(c+d)) |
|
|
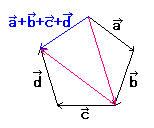
(a+((b+c)+d)) |
|
|
(a+(b+(c+d))) |
|
5角形のばあいは、頂点(ちょうてん)の個数と同じになってしまい、
つまらなかったですね。
ぜひ、6角形あたりでやってみてください。
5 のつぎのカタラン数というと
1 , 1 , 2 , 5 , 14 , 42 , ・・・
ですから、14 です。
6角形で、ちゃんと14通りみつかりましたか。
● おつりの問題 ●
カタラン数は、いろいろなところで出てきます。
そのひとつが、「おつりの問題」です。
たとえば・・・
| 【問題】 6人からお金をあつめます。 1人50円ずつあつめます。 3人は50円玉、3人は100円玉をもってきました。 おつりがたりなくならないような、 お金のあつめ方の順番は何通りありますか。 ただし、お金の金額(きんがく)のみを考え、
|
かんたんですね。
「50円玉」 を 「( 」
「100円玉」 を 「+」
に対応させれば、同じ問題になります。
道順でいえば、とちゅう1度もそんをしない、
つまりず〜っと上の方を通っていく行き方の個数です。
だから、さっきと同じ 5通りです。
(((+++ 50 50 50 100 100 100
((+(++ 50 50 100 50 100 100
((++(+ 50 50 100 100 50 100
(+((++ 50 100 50 50 100 100
(+(+(+ 50 100 50 100 50 100
ところで、このホームページの「カタラン数(1)」で
こんなことを考えました。
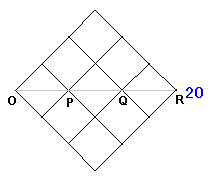
ぜんぶで20通りのうち、ついている「わりあい」が
3/3 つまり ず〜っと上 は 5通り
2/3 つまり 2/3上 で 1/3下 も 5通り
1/3 つまり 1/3上 で 2/3下 も 5通り
0/3 つまり ず〜っと下 も 5通り
でした。
これを、今の「おつりの問題」にあてはめると
おつりがたりなくならない は 5通り
1回おつりがたりなくなる も 5通り
2回おつりがたりなくなる も 5通り
3回おつりがたりなくなる も 5通り
となってきます。
じっさい、こうなりますね。
|
<0回> 50 50 50 100 100 100 50 50 100 50 100 100 50 50 100 100 50 100 50 100 50 50 100 100 50 100 50 100 50 100
|
<1回> 50 50 100 100 100 50 50 100 50 100 100 50 50 100 100 50 50 100 100 50 50 50 100 100 100 50 50 100 50 100
|
|
<2回> 50 100 100 100 50 50 50 100 100 50 100 50 100 50 50 100 100 50 100 50 100 50 50 100 100 100 50 50 50 100
|
<3回> 100 100 100 50 50 50 100 100 50 100 50 50 100 100 50 50 100 50 100 50 100 100 50 50 100 50 100 50 100 50
|
カタラン数は、ほかにもいろいろ出てきます。
たとえば、コンピュータのプログラミングなどで、
( )の個数があわないと、エラーになりますね。
この正しい ( ) のつけ方(?)もカタラン数になります。
たとえば、( )を3つ使うばあいは、「+」を「) 」におきかえるだけです。
(((+++ ・・・ ( ( ( ) ) )
((+(++ ・・・ ( ( ) ( ) )
((++(+ ・・・ ( ( ) ) ( )
(+((++ ・・・ ( ) ( ( ) )
(+(+(+ ・・・ ( ) ( ) ( )
カタラン数がでてくるのは、まだまだ、たくさんあります。
いちど、さがしてみてください。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001