フラクタル次元　～さんすう・数学のお勉強～

フラクタル次元

●　次元　●

　「４次元」というと、まるでＳＦ小説のようで大人気です。

　だったら、「分数や小数の次元」ともなると、
もっともっと人気がでてきそうです。

　まあ、ねらったわけでもないでしょうが、
そんな次元を考えて大人気となった（？）数学者がいたのですから、
世界は広いですね～。

　まずは、ふつうの（？）次元をふりかえってみます。

　１次元からです。

　

２倍に拡大すると
（長さを２倍にすると）、
もとの図形が２つできます。
　　２^１＝２

この図形は１次元と考えよう！

　うん、いいですね。

　

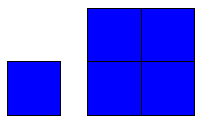
２倍に拡大すると
（長さを２倍にすると）、
もとの図形が４つできます。
　　２^２＝４

この図形は２次元と考えよう！

　なかなか、いいですね。

　

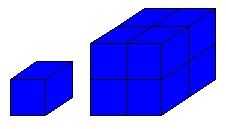
２倍に拡大すると
（長さを２倍にすると）、
もとの図形が８つできます。
　　２^３＝８

この図形は３次元と考えよう！

　またまた、いいですね。

●　フラクタル次元　●

　１次元より小さい次元も、
こんなふうにすれば考えられます。

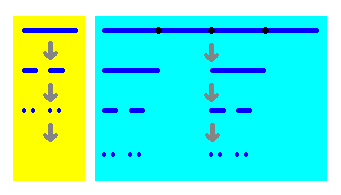４倍に拡大すると
（長さを４倍にすると）、
もとの図形が２つできます。

　　４^ｘ＝２

この図形はｘ次元と考えよう！

　もちろん、もとの図形も拡大（かくだい）した図形も、
ず～っと穴（あな）をあけていってできた図形のつもりです。

　つまり、前回とりあげた「ガスケット」ですね。

　さて、

　　　　　　　　　４^ｘ＝２

　のｘにあてはまる数は何でしょう。

　高校生なら、「指数・対数」のところでお勉強したので、
わかりますよね。

　中学生でも、何回か「かけ算」した数ということで

　　　　　　　　　４^０＝１

　　　　　　　　　４^１＝４

　　　　　　　　　４^２＝１６

　　　　　　　　　４^３＝６４

のように、かけ算した回数が整数（せいすう）ならわかりますよね。

　じつは、

　　　　　（４^２）^３＝４^２×３　

のような指数法則がなりたつように、分数まで広げてお約束するのです。

　　　　　　　　　４^ｘ＝２

　　　　　　　　　（２^２）^ｘ＝２^１

　　　　　　　　　２^２ｘ＝２

ということで、

　　　　　　　　　　　２ｘ＝１

　　　　　　　　　　　ｘ＝１/２

と約束するのです。

　けっきょく、こんなおもしろい次元の考え方をすると
１/２次元（０．５次元）となることがわかりました。

　もちろん、次元というものはこんなふうに考えなくっちゃいけない・・・
なんていう話ではありませんよ。

　あくまでも、こんな考え方もできるということです。

●　ガスケット　●

　前回の「ガスケット」で、シェルピンスキー・ガスケットと

２倍に拡大すると
（長さを２倍にすると）、
もとの図形が３つできます。

　　２^ｘ＝３

この図形はｘ次元と考えよう！

（ｘは高校で習いますよ。）

さらに上の三角形もとりのぞいたものを考えました。

２倍に拡大すると
（長さを２倍にすると）、
もとの図形が２つできます。

　　２^１＝２

この図形は1次元と考えよう！

　そして、あとの方の図形は、どんどん直線（線分）に近づいて行きそうだな～
というところで終わってしまいました。

　でも、この次元の考え方では、ちゃ～んと1次元ということになって、
なかなかうまい考え方だな～って思いますよね。

●　１．５次元　●

　さきほどは、１/２次元（０．５次元）というのをやりましたから、
今度は３/２次元（１．５次元）というのをやりましょう。

　ぎゃくに考えて、

　　　　　　　　　　　ｘ＝３/２

　　　　　　　　　　　２ｘ＝３

　　　　　　　　　２^２ｘ＝２^３

　　　　　　　　　（２^２）^ｘ＝２^３

　　　　　　　　　４^ｘ＝８

　ですから、４倍に拡大すると（長さを４倍にすると）、
もとの図形が８つできるようにしましょう

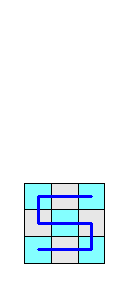
　「ガスケット」なら、こんなふうにすればいいですね。

　たてを見ると、ふつうの１次元
よこを見ると、さっきの１/２次元（０．５次元）というものです。

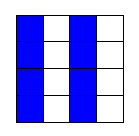
　これを、ず～っとくりかえしたものは、

　　　　　１＋１/２＝３/２　次元

となります。

　さて、「ガスケット」はぬきとって、つまりへらして考えましたが、
はんたいに、ふやして考えてみましょう。

　ふやすといっても・・・

　そう、直線なら平面にはみだしてくるってことになります。

　ですから、４倍に拡大すると（長さを４倍にすると）、
もとの図形が８つできるようにするには・・・

　たとえば、こんなふうなものを考えます。

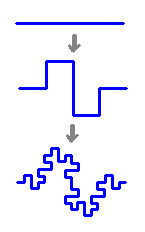
　そして、あの「コッホ曲線」は、
このふやした方の曲線です。

　あの「コッホの雪片」は、
こんな「コッホ曲線」でかこまれていましたね。

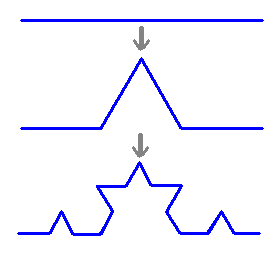
　これは、３倍に拡大すると（長さを３倍にすると）、
もとの図形が４つできますから・・・

　　　　　　　　　３^ｘ＝４

となるようなｘ次元です。（ｘは高校で習いますよ。）

●　ペアノ曲線　●

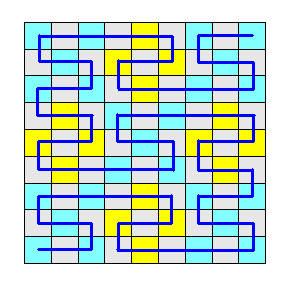
　さいごに、平面を１本の直線でうめつくした
「ペアノ曲線」をみてみましょう。

　これは、３倍に拡大すると（長さを３倍にすると）、
もとの図形が９つできていますから・・・

　　　　　　　　　３^２＝９

　ほら、ちゃ～んと２次元となりますね。

●　おわりに　●

　ここまできたら、次は５/２次元（２．５次元）だ～
といいたいところですが・・・

　図をかくのがたいへんなので（？）、やめにしましょう。

　立方体に穴（あな）をあけていって作る
「ガスケット」なら、かんたんですね。

　立体の表面をつきだしていく方は、いかがでしょうか。

　でも、５/２次元（２．５次元）にはこだわることもないですね。

　それでは、「夏休みの作品」にすてきな図形を作ってみてください。

HOME（もどる）