フィボナッチ数
● ユークリッドの互除法 ●
<お勉強>の「黄金数」ででてきたように、
フィボナッチ数というのは、こんな数でした。
1,1,2,3,5,8,13,21,34,55,・・・
これらの数はこんなふうにして出てきました。
1
1
1+1=2
2+1=3
3+2=5
5+3=8
・・・・・・・
これって、じつはユークリッドの互除法です。
<お勉強>の「ユークリッドの互除法」のところで、
(ずばり 5 と 8 で)一度やったのです。
ユークリッドの互除法って、お互いにわり算していくのでしたから、
8÷5=1 あまり 3
5÷3=1 あまり 2
3÷2=1 あまり 1
となります。
これの「たしかめ算」は
8=1×5+3 つまり 8=5+3
5=1×3+2 つまり 5=3+2
3=1×2+1 つまり 3=2+1
これに
2=1+1
をつけくわえると、これはもう
(下から見ていけば)フィボナッチ数の出し方ですね。

ユークリッドの互除法では、最大公約数をもとめたのですから、
この場合は、5と8の最大公約数が1ということです。
このとき、5と8は 互いに素 っていいましたね。
ということは・・・
5 と 8 でなくっても、フィボナッチ数のとなりあった数であれば、
(作り方をさかのぼっていけば、それがユークリッドの互除法になっていて)
最大公約数は 1 とわかります。
つまり、フィボナッチ数のとなりあった数は、互いに素になっています。
● フィボナッチ数の性質(1) ●
フィボナッチ数 1,1,2,3,5,8
について、すぐにこんなことがわかります。

長方形の面積は、正方形の面積をあわせたものですから
12+12+22+32+52 = 5×8
となります。
フィボナッチ数 1,1,2,3,5,8,13,21,34,55
についても同じようにしてやれば、
12+12+22+32+52+82+132+212+342= 34×55
となります。
つまり、
フィボナッチ数をじゅんに2乗してたすと、最後とその次の数をかけたもの
になるのですね。
● フィボナッチ数の性質(2) ●
フィボナッチ数 1,1,2,3,5,8
について、すぐにこんなこともわかります。
8=5+3
5=3+2
3=2+1
2=1+1
ここで、つぎつぎに下の式を入れていくのです。
そうすると、
8=(3+2)+3
=(2+1)+2+3
=(1+1)+1+2+3
これより、
8−1=1+1+2+3
つまり
1+1+2+3 = 8−1
となります。
フィボナッチ数1,1,2,3,5,8,13,21,34,55
についても同じようにしてやれば、
1+1+2+3+5+8+13+21 = 55−1
となります。
つまり、
フィボナッチ数をじゅんにたすと、最後の次の次の数から1ひいたもの
になるのですね。
● フィボナッチ数の性質(3) ●
それなら、今度はひとつおきにたしてみましょう。
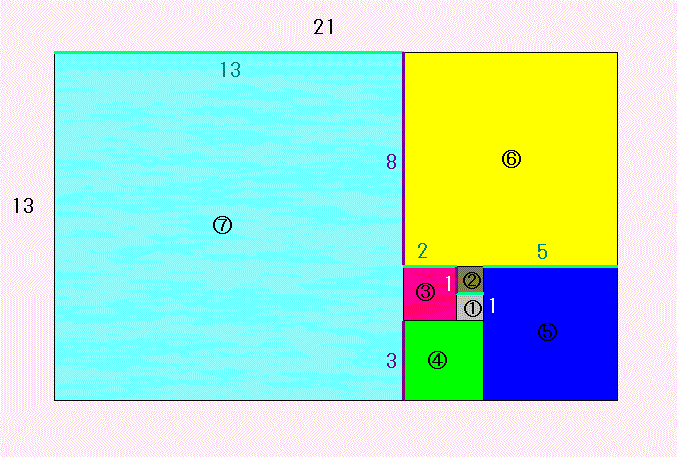
フィボナッチ数 1,1,2,3,5,8,13,を、ひとつおきにたすのです。
つまり、
1+2+5+13=?
1+3+8=?
を考えるのです。
<横の長さ>
1+2+5+13=?
これは、ちょうど
1番と3番と5番と7番の正方形の辺の長さをあわせたもの
になっていますから、大きい長方形の横の長さの 21 になります。
フィボナッチ数 1,1,2,3,5,8,13,の次の数の 21 です。
1+2+5+13=21
フィボナッチ数 1,1,2,3,5,8,13,21,34,(55)
についても同じようにしてやれば、
1+2+5+13+34=55
となります。
つまり、
奇数番目のフィボナッチ数をじゅんにたすと、最後の次の数
になるのですね。
<たての長さ>
1+3+8=?
これは、ちょうど
2番と4番と6番の正方形の辺の長さをあわせたものにあと1たすと
大きい長方形のたての長さの 13 になります。
ですから、
1+3+8=13−1
フィボナッチ数 1,1,2,3,5,8,13,21,34,(55)
についても同じようにしてやれば、
1+3+8+21=34−1
となります。
つまり、
偶数番目のフィボナッチ数をじゅんにたすと、最後の次の数から1ひいたもの
になるのですね。
● フィボナッチ数の性質(4) ●
今度は、ちょっとだけむずかしい(?)こんなことを考えます。
フィボナッチ数 1,1,2,3,5,8
について、じつはこんなことも知られています。
(ほかにもずいぶんいろいろ研究されているらしいのですが・・・。)
まず、最初の3つの 1,1,2 について、
外2つをかけたのから中の2乗をひいてみます。
1×2−12=1
おなじようにして、次の3つの 1,2,3 についてやってみます。
1×3−22=−1
おなじようにして、
2×5−32=1
3×8−52=−1
どうも、たがいちがいに 1 と −1 がでてくるようです。
では、このことを見てみましょう。
< 1×3−22=−1 >
面積で考えるのです。
ポイントは、2つの図形の面積のちがいは
それぞれに等しい面積をつけくわえてもかわらないってことです。
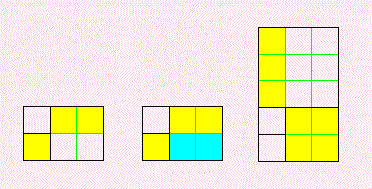
上の左の図で、
1×2 は 黄色い長方形の面積です。
12 は 黄色い正方形の面積です。
まず、
1×2−12=1
は、(ちょくせつ)計算しておきます。
両方に、青い長方形の面積 1×2 をたします。
1×2−12 = 1×2+1×2−(12+1×2)
= (1+1)×2 − 1×(1+2)
= 2×2 − 1×3
= 22 − 1×3
そうすると、今度は上の右の図で、
22 は 黄色い正方形の面積です。
1×3 は 黄色い長方形の面積です。
ここで、
1×2−12 は長方形から正方形をひいたもの
22 −1×3 は正方形から長方形をひいたもの
というふうに、正方形と長方形が入れかわることに注意してください。
けっきょく、
1×2−12 = 22−1×3
となりましたね。ですから、
1 = 22−1×3
つまり、
1×3−22=−1
< 2×5−32=1 >
どんどん、やってみましょう。
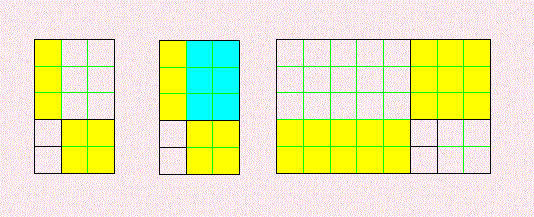
上の図から、同じようにして、
1×3−22 = 32 −2×5
−1 = 32 −2×5
これより、
2×5−32 = 1
< 3×8−52=−1 >
これも、同じようにやれますね。
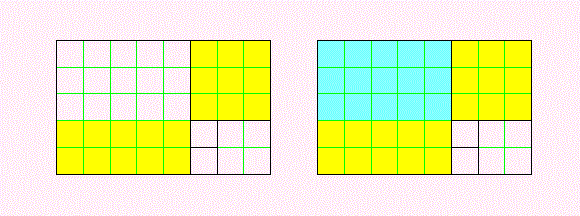
けっきょく、次々にやっていけば
3つ続いたフィボナッチ数の、外2つをかけたものから中の2乗をひくと、
(かわりばんこに) 1 か −1
になるのですね。
< 行列式 >
行列式を知っているって人は、いまやっていたことはこんなことですね。
(じつは、フィボナッチ数の一般項やこの性質は、
大学でお勉強する「線形代数」っていう一般論からでてくるのです・・・。)
|1 1| |1+1 1| |2 1| |1 2|
| | = | | =
| | = − | |
|1 2| |1+2 2| |3 2| |2 3|
|1 2| |1+2 2| |3 2| |2 3|
| | = | | =
| | = − | |
|2 3| |2+3 3| |5 3| |3 5|
|2 3| |2+3 3| |5 3| |3 5|
| | = | | =
| | = − | |
|3 5| |3+5 5| |8 5| |5 8|
● フィボナッチ数列の一般項 ●
フィボナッチ数というのは、こんな数でしたね。
1,1,2,3,5,8,13,21,34,55,・・・
数がずら〜っと列をなしてならんでいるので(?)、こういうのを数列っていうのです。
そして、このフィボナッチ数列のようにきそく正しい数列は、
あてはめるだけでパッと答えがでてくるという、公式のようなものをさがそうとするのです。
そんな公式は、次のような式で知られています。
1 n
n
Fn = /5 (α − β ) ・・・ (1)
ここで、αとβは、黄金数をもとめた2次方程式(4)の正の解と負の解です。
<お勉強>の「黄金数」でやったことをもう一度かくと、
1
X = 1 + X ・・・ (2)
X2 = X + 1 ・・・ (3)
X2 − X − 1 = 0 ・・・ (4)
この2次方程式を解くと
1+/5 1−/5
X= 2 , 2
ですから、
1+/5 1−/5
α= 2 , β= 2
この公式のnに何番目かを入れてやると、パッとフィボナッチ数がでてくるはずです。
(といっても、3乗や4乗してたしかめてみたくはありませんよね・・・)
n=1 を入れると F1=1
n=2 を入れると F2=1
n=3 を入れると F3=2
n=4 を入れると F4=3
n=5 を入れると F5=5
n=6 を入れると F6=8
じつは、このようなお話は
高校では「漸化式」のところで、大学では「線形代数」でやるようなお話ですが、
今回は何も使わないでやりましょう。
● 黄金数でフィボナッチ数列 ●
フィボナッチ数
1,1,2,3,5,8,13,21,34,55,・・・
はこんなふうにして出していきましたね。
1
1
1+1=2
2+1=3
3+2=5
5+3=8
・・・・・・・
そこで、最初2つを 1,1 でなくて、
1,α から始めて同じように数列をつくっていきます。
1
α
α+1=?
さあ、ここで α+1=? は何でしょう。
α が 2次方程式(3)の解ということは
α2 = α + 1 ・・・ (5)
ということですから、α+1=α2 です。
では、その次の α2+α=? は何でしょう。
(5)の両辺に αをかければ
α3 = α2 + α ・・・ (6)
ですから、α2+α=α3 となります。
つまり、こうなります。
1
α
α+1=α2
α2+α=α3
α3+α2=α4
α4+α3=α5
・・・・・・・
そうすると、黄金数版フィボナッチ数列(こんな言葉はありませんのでご注意)は、
こんなふうになります。
1,α,α2 ,α3 ,α4 ,α5 ,・・・・・
もうひとつの解の β についてもおなじようにして
1,β,β2 ,β3 ,β4 ,β5 ,・・・・・
となります。
ここで、この2つの数 α,β については、何番目の数でも
パッとだせる公式をつくるのはかんたんですね。
そこで、フィボナッチ数をこの2つの数 α,β を使って
どうかけるかを考えていくのです。
● フィボナッチ数とリュカ数 ●
さあ、今度はじっさいに
1,α,α2 ,α3 ,α4 ,α5 ,・・・・・
1,β,β2 ,β3 ,β4 ,β5 ,・・・・・
を計算してみましょう。
えっ、3乗や4乗なんてしたくない?
だいじょうぶ!だいじょうぶ!
そのために(?)、α+1=α2 ,α2+α=α3 があるのです。
α0=1
1+1/5
α = 2
2 1+1/5 1+1/5 2 3+1/5
α = 2 + 1 = 2 + 2 = 2
3 3+1/5 1+1/5 4+2/5
α = 2 + 2 = 2
4 4+2/5 3+1/5 7+3/5
α = 2 + 2 = 2
5 7+3/5 4+2/5 11+5/5
α = 2 + 2 = 2 ・・・ (7)
ここで、/5 にかけてある数 1,1,2,3,5 は
フィボナッチ数であることに気づきますね。
ちなみに、1,3,4,7,11 も 1 と 3 から始めて
フィボナッチ数と同じようにつくられていますね。
こちらの方は、リュカ数とよばれています。
さて、今度は β についても同じようにやってみましょう。
β0=1
1−1/5
β = 2
2 1−1/5 1−1/5 2 3−1/5
β = 2 + 1 = 2 + 2 = 2
3 3−1/5 1−1/5 4−2/5
β = 2 + 2 = 2
4 4−2/5 3−1/5 7−3/5
β = 2 + 2 = 2
5 7−3/5 4−2/5 11−5/5
β = 2 + 2 = 2 ・・・ (8)
さて、ここでたとえば 5番目のフィボナッチ数 F5=5 をだしたいとします。
(7)と(8)の式をひいてみると
5 5 11+5/5 11−5/5
α − β = 2 − 2 = 5/5
これより
1 5 5
/5 (α − β ) = 5
とでます。ほかも同じようにしてでますね。
ちなみに、リュカ数の方はもっとかんたんで
5 5 11+5/5 11−5/5
α + β = 2 + 2 = 11
のようにして、たすだけででますね。
フィボナッチ数は、自然の中にずいぶんと見られるそうです。
ぜひ、調べてみてください。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001