ガスケット　～さんすう・数学のお勉強～

ガスケット

●　シェルピンスキー・ガスケット　●

　「ガス」といったら何を想像（そうぞう）しますか。

　えっ、「おなら」？

　じつは、「gaseous」（ガスのような）という英語に
こんな意味（いみ）があったのです。

　「空虚（くうきょ）な」
　「実質（じっしつ）のない」
　「むなしい」・・・

　どうも、「スカスカでなかみがない」ようすを表しているようです。

　「ガスケット」というのは、そんなスカスカしたものです。

　では、はじめにシェルピンスキー・ガスケットのしょうかいをしましょう。

　まず、正三角形を用意（ようい）します。

　べつに、正三角形である必要（ひつよう）はありませんが・・・。
　まあ、どんな三角形でもいいのです。
　そのときは、中点連結定理というものがありますからね。

　これから、まん中をぬきとって、スカスカにしていきます。

　もちろん、ぬきとる方はどうでもいいのですが、
のこったものは、もとの三角形を小さくしただけで形が同じ、
つまり相似（そうじ）というのがポイントです。

　いまは、長さを１/２にしたもの、
つまり相似比が１/２の三角形が、３つできました。

　これを、くりかえすのです。

　どんどん、どんどん・・・

　まあ、こんなちょうしで、ず～っと穴（あな）をあけていくのです。

　スカスカしていて、風通しがよさそうですね。

　なんだか、「レースあみ」や「切り紙細工」を思い出します。

●　「１＋１＝１？」　●

　このホームページで、「１＋１＝１？」というのをやりましたね。

　そこでは、こんな図をもとにしていました。

　それでは、これとよく似（に）たことを、
「ガスケット」でやってみましょう。

　シェルピンスキーのガスケットでは、
まん中をぬきとって、スカスカにしていきましたが、
今度は、上の三角形もぬきとってしまいます。

　左がシェルピンスキーのガスケットで、
右が今回のものです。

　

はじめは同じ

　

左は３つ
右は２つ

同じ
くりかえし

　これをず～っとくりかえすと、なんだか直線になっていきそうです。

　ペアノ曲線では、直線が平面をうめつくしそうだったのに、
今度は平面に穴（あな）をあけていくと、どんどん直線になりそうです。

●　「ガスケット」作り　●

　「ビスケット」作りは、むずかしいのかもしれませんが、
「ガスケット」作りならかんたんです。

＜　正方形　＞

　まずは、正方形です。

　まん中に穴（あな）をあけてみましょう。

　もちろん、もっと他にぬきとってもかまいません。
　そうすれば、もっと風通しがよくなるってものです。

　くりかえしますが、ぬきとる方はどうでもいいのですが、
のこったものは、もとの正方形を小さくしただけで形が同じ、
つまり相似（そうじ）というのがポイントです。
　（まあ、正方形ならみんな相似ですけれどね。）

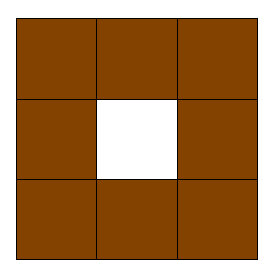
　今度は、長さを１/３にしたもの、
つまり相似比が１/３の正方形が、８つできました。

　これを、くりかえすのです。

　もちろん、もっとず～っとくりかえすのです。

＜　正六角形　＞

　次は、正六角形です。

　今度は、まん中でなくって、まわりに穴（あな）をあけてみましょう。

　もちろん、もっと他にぬきとってもかまいません。
　そうすれば、もっと風通しがよくなるってものです。

　今度は、ぬきとるのがまん中ではないし、
おまけに、ぬきとった形が正六角形でもありません。

　でも、そんなことはど～でもいいことなのです。

　ぬきとる方ではなくって、
のこったものが、もとの正六角形を小さくしただけで形が同じ、
つまり相似（そうじ）というのがポイントです。
　（まあ、正六角形ならみんな相似ですけれどね。）

　今度は、長さを１/３にしたもの、
つまり相似比が１/３の正六角形が、７つできました。

　正方形のときは、相似比が１/３の正方形が、８つできたのですから、
まあ、１つ少ないってことからも、よりスカスカしたものができそうですね。

　くりかえしてみましょう。

　どうですか。

　何か気づきませんか。

　のこった方ではなくって、穴（あな）の方をみつめてみましょう。

　そうです。

　「コッホ曲線」です。

　穴（あな）のまわりに、あっちにもこっちにも、
コッホ曲線がみつかります。

　そして、その穴（あな）自身は、コッホ曲線でかこまれた
「コッホの島」（「コッホ雪片」）というものになっています。

＜　正五角形　＞

　次は、正五角形です。

　今度も、まん中でなくって、まわりに穴（あな）をあけてみましょう。

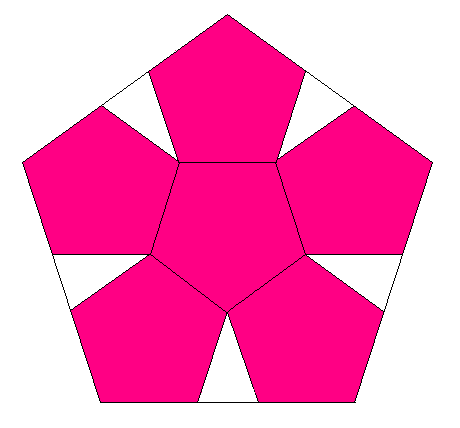
　今度の相似比がいくらかは、
このホームページの「ペンタグラム」をみてください。

　あの黄金数の登場（とうじょう）となります。

　では、くりかえした図形をみてみましょう。

　まあ、きれいに花がさいたみたい。

　ますます、「レースあみ」や「切り紙細工」を思い出しますね。

HOME（もどる）