黄金数　～さんすう・数学のお勉強～

黄金数

●　黄金数　●

　数といったら、なんといっても黄金数です。

　数の中のキング、いえ、連分数の中のキングともいうべき数です。
　（連分数については＜お勉強＞の「連分数」をみてね。）

　　　　　　これぞ連分数の中の連分数！

と、いったところでしょうか。

　で、どんな数？

　もちろん（？）黄金数というのは、連分数であらわすと、ず～っと　１　が続く数です。

　　　　　　　　　　　　　　　１　　　　　　　　
^１　＋　　　　　　　１　　　　　　
　　　　　　　　　　　１＋　　　　　　１　　　　
　　　　　　　　　　　　　　^１^＋１＋
　　　　　　　　　　　　　　　　　　　　・・・

　ちなみに、連分数であらわすと、ず～っと　２　が続く数は、
前回の　/２　に　あと　１　たした

　　　　　　　　　　　　　　　　　　　　　　１　　　　　
　　　　^{１　＋　/２　＝　２　＋}　　　　　　１　　　　
　　　　　　　　　　　　　　　　　　２＋　　　　　１　　　　
　　　　　　　　　　　　　　　　　　　　　^２＋２＋
　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・

です。

　では、これから黄金数をもとめてみましょう。

　まず、

　　　　　　　　　　　　　　　　　　　　　１　　　　　　　　
　　　　　　^{X　　＝　１　＋}　　　　　　　１　　　　　　
　　　　　　　　　　　　　　　　　１＋　　　　　　　１　　　　
　　　　　　　　　　　　　　　　　　　　　^１＋１＋
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・

とおくと、

　　　　　　　　　　　　　　　　　　１　
　　　　　　^{X　　＝　１　＋}　　X　　　　・・・　（１）

　これから、

　　　　　　X^２　＝　X　＋　１

　　　　　　X^２　－　X　－　１　＝　０

　この２次方程式を解くと

　　　　　　　　^１＋/５　　　　　　^１－/５　　
　　　　　^X＝　２　　　　　，　　　２　　　　

　　　　　　　　^１＋/５　　　　　　　　^{－１＋/５}　
　　　　　^＝　２　　　　　，　^－　　２　　　　

　このうちの正の数の方が、もとめていたものです。
　（負の数の方も、マイナスをとったものがあとで出てきますよ。）

　つまり、黄金数というのは、

　　　　　　^１＋/５　　　　　　　　　　　　　　１　　　　　　　　
　　　　　　２　　　　^{＝　１　＋}　　　　　　　１　　　　　　
　　　　　　　　　　　　　　　　　　　　１＋　　　　　　　１　　　　
　　　　　　　　　　　　　　　　　　　　　　　　^１^＋１＋
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・

です。

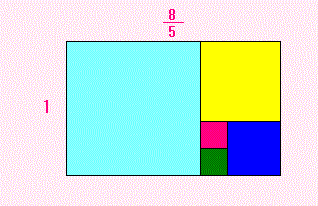
　さて、連分数にあらわすと、ず～っと　１　が続くっていうのは、
こんなことでしたね。
　（ちょっと図がくるっていますが・・・。
　まん中のところは、ず～っと同じことのくりかえしになっていると思って見てください。）

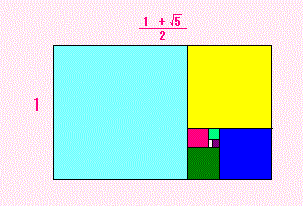
　上の図のような長方形から、どんどん（なるべく大きな）正方形をとっていくと、
正方形は　いつも　１個　とれては　「はんぱ」　がでるんだけど、
その「はんぱ」の長方形がみ～んな相似なのでした。

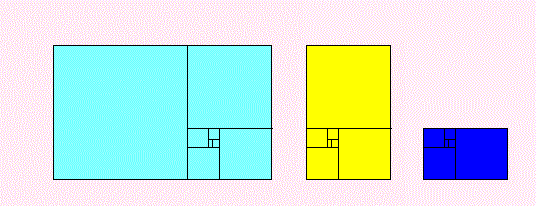
　でも、これって　いつもの黄金比（黄金分割）とちょっとちがうな～
って、思っていませんか。

　黄金分割って、こんなふうにして　長さ１　を分割するのでした。

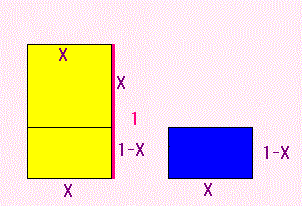
　長方形の、長い方の辺の長さを　１　にします。
　ここから、正方形を切り取るのですが

　　　のこった長方形が、もとの長方形と相似になるように

するには、どこで切ったらよいか
　（これって、ず～っと１が続く連分数にしたいってことよね～）

　・・・ということで、このときの長さの比が、黄金比でした。
　そして、その比の値が黄金数です。

　図でいうと

　　　　　１　：　X　＝　X　：　１－X

となる　X　が黄金数で、　１：X　（つまり　X：１－X　）が黄金比です。

　それだったら、さっきの２つ目の長方形が、まさしくそうなっていますよね。

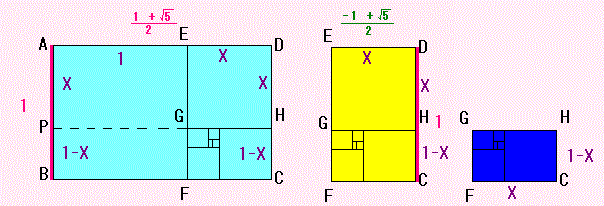
　ですから、

　　　　X　＝　^１＋/５　　_－　１
　　　　　　　　　２　　　　

　　　　　　＝　　^{－１＋/５}　
　　　　　　　　　　　　２　　　　

　ほらっ、どっかで見たことあるでしょ。
　そう、さっきの２次方程式の負の数の解のマイナスをとったものです。

　さらに、これを連分数であらわすと、１　へるだけですから

　　　　　　^{－１＋/５}　　　　　　　　　　　　１　　　　　　　　
　　　　　　　２　　　　^＝　　　　　　　　　１　　　　　　
　　　　　　　　　　　　　　　　　　　　１＋　　　　　　　１　　　　
　　　　　　　　　　　　　　　　　　　　　　　　^１^＋１＋
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・

　な～んだ。
　けっきょく、長方形のたてを１にするか、横を１にするかのちがいだけだ・・・
ということで、どちらも黄金数とよんでいるようです。

●　フィボナッチ数　●

　さて、フィボナッチ数というのは、こんな数です。

　　　　　１，１，２，３，５，８，１３，・・・

　最初の数は　　１
　次の数も　　１
　その次の数は、この２つをたすと　１＋１＝２　なので　　２
　その次の数は、この２とその前の１をたすと　２＋１＝３　なので　　３
　その次の数は、この３とその前の２をたすと　３＋２＝５　なので　　５
　その次の数は、この５とその前の３をたすと　５＋３＝８　なので　　８
　その次の数は、この８とその前の５をたすと　８＋５＝１３　なので　　１３

　こんなふうにして、次々にでてくる数がフィボナッチ数です。

　　　　　１，１，２，３，５，８，１３，・・・

　そこで、フィボナッチ数　１，１，２，３，５，８，１３，・・・　のうちの
たとえば、５　と　８　を図にしてみます。

　さらに、この図を１/５（５分の１）に縮小して、スケールをそろえます。

　そうして、もう一度ならべてみます。

　どうですか。
　にてますよね～。

　それもそのはず。じつは、

　　　　　黄金数　　^１＋/５　
　　　　　　　　　　　　２　　　　

の分数の近似値が

　　　　　フィボナッチ数の比の値　　^８^５　

になっているのです。

　もちろん、フィボナッチ数の　５　と　８　でなく、もっと後の方の数のほうが、
もっとよい近似値になっています。

　では、これからこの関連をみていきましょう。

●　近似分数　●

　さて、連分数のとちゅうまで計算して（のこりは切り捨てて）
分数で近似するというのをやりましたね。

　黄金数

でやってみましょう。

　とちゅうまでの分数を計算しますね。

　　　　　　　X_１　　＝　１

　　　　　　　　　　　　　　　　　　１　　　　　　　　　１　　　　　１＋１　　　　２　
　　　　　　^X_２^{＝　１　＋}　X_１　　^＝　１＋１　　　^＝　１　　　＝　１

　　　　　　　　　　　　　　　　　　１　　　　　　　　　１　　　　　２＋１　　　　３　
　　　　　　^X_３^{＝　１　＋}　X_２　　^＝　１＋２　　　^＝　２　　　＝　２

　　　　　　　　　　　　　　　　　　１　　　　　　　　　２　　　　　３＋２　　　　５　
　　　　　　^X_４^{＝　１　＋}　X_３　　^＝　１＋３　　　^＝　３　　　＝　３

　　　　　　　　　　　　　　　　　　１　　　　　　　　　３　　　　　５＋３　　　　８　
　　　　　　^X_５^{＝　１　＋}　X_４　　^＝　１＋５　　　^＝　５　　　＝　５

　さて、ここで　分子の　１＋１，２＋１，３＋２，５＋３　を見てみましょう。

　これって、フィボナッチ数の作り方そのものですね。
　ですから、黄金数の近似分数の分子と分母には、
つぎからつぎへとフィボナッチ数がでてくるのです。

　ついでに、黄金数をもとめた　（１）の式

　　　　　　　　　　　　　　　　　　１　
　　　　　　^{X　　＝　１　＋}　　X　　　　・・・　（１）

も、もう一度ながめてみましょう。

　これをみても、

　　　　　黄金数とフィボナッチ数は、おおいに関係あり！

って思いますよね。

　ということで、次回は「フィボナッチ数」についてです。
　おたのしみに！！

HOME（もどる）