グラフ　～さんすう・数学のお勉強～

グラフ

●　数える　●

　あなたが、生まれてはじめて数えたものは何ですか。

　「さあ、おめめは、いくつあるかな～？」　・・・　「ふた～つ」
　「では、お口は、いくつあるかな～？」　・・・　「ひと～つ」
　「まあ、かしこいわね～！」

　でも、もし・・・
　かた方の目が、頭のうしろの方についていたらどうなったでしょう。

　「さあ、おめめは、いくつあるかな～？」　・・・　「ひと～つ」
　（くるりとまわって）「あら、こっちにもう１つあるでしょ！」　・・・　「うぇ～ん」

　人生のスタートから、さんすうにつまずいていたかもしれません。

　そういえば、正多面体の頂点や辺だって、
顔のように前の方にあつまっていると数えやすいのに・・・

　それに、絵にもかきやすいってものです。（ピカソはべつとして・・・）

　だったら、あつめてしまいましょう。

　そうです。このホームページでもやりましたね。

　　数をかぞえる時に大切なこと
それは、「数え落としをしない」ということと
「おなじものを、二度かぞえない」ということでした。

　たとえば、交点の個数を数えるとき、
直線はまっすぐである・・・なんて、ど～でもよかったですね。

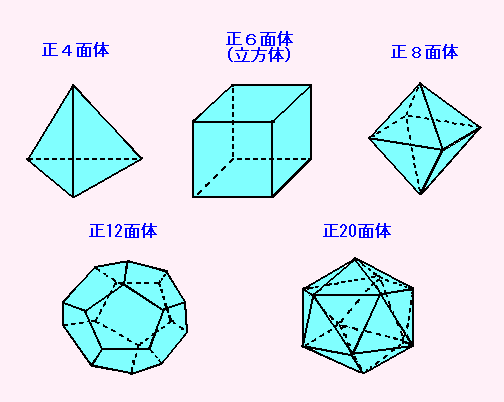
　さあそれでは、３次元の正多面体を２次元の平面にかいてみましょう。

　もちろん、下のような見取り図（みとりず）のことではありませんよ。
　頂点や辺を、顔のように前の方へあつめて、
顔だけスケッチしたいのです。

　そして、その次には・・・
４次元の超立方体を３次元の空間にスケッチしてみたいものですね。

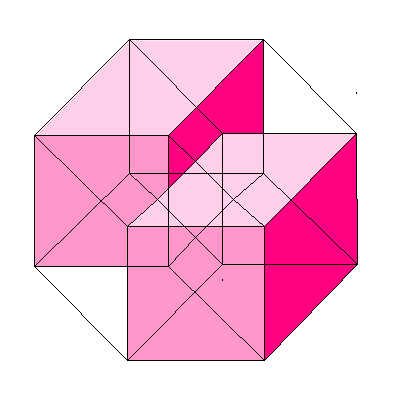
●　正多角形　●

　まず、リハーサルとして、
２次元の正多角形を１次元の直線にスケッチすることからはじめましょう。

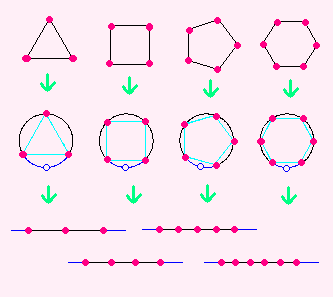
　どれも、いちど円にしてから、１つの辺の１点をぬきとって
ぴよ～んってのばせば、スケッチのできあがりです。

　これを使って、
１次元しか知らない人間に、２次元の正多角形をおしえるとどうなるでしょう。

＜１次元の教室にて＞

先生：　「今日は、２次元の正多角形というものをお勉強しますよ。
　　　　　ここから、ず～っと前に進むと、頂点にぶつかるわね。
　　　　　そのあと目にした「ふうけい」をおぼえておくのよ。
　　　　　そこからまた、ず～っと前に進むと、また頂点にぶつかるわね。
　　　　　そのあと目にした「ふうけい」は、さっきのと同じでしょ。
　　　　　そこからまたまた、ず～っと前に進むと、またまた頂点にぶつかるわね。
　　　　　そのあと目にする「ふうけい」は、さっきとちがうでしょ。
　　　　　でも、２次元の正多角形では、これが同じ「ふうけい」に見えるの。
　　　　　それに、この１次元の世界では、ここから先へず～っと進んでも、
　　　　　どこまでいっても、もといたところにもどれないでしょ。
　　　　　でも、２次元の正多角形というのはね、
　　　　　なんと、もといたところにもどれるのよ。
　　　　　ず～っと前と、ず～っとうしろは、
　　　　　無限（むげん）のかなたで、つながっているって考えるのよ。
　　　　　そして、そのつながってできたところで見える「ふうけい」は、
　　　　　さっきの「ふうけい」と同じなの。」

せいと：　「？？？」

先生：　「それに、この１次元の世界では、「みどり」のところを通らずに、
　　　　　「はい色」のところへワープしたりできないでしょ。
　　　　　でもね、２次元の世界ではできるのよ。

せいと：　「？？？？？」

●　正多面体　●

　それでは次は、３次元の正多面体を２次元の平面にスケッチしてみましょう。

　もちろん、２次元しか知らない人間に、
３次元の正多面体ってものをおしえられるようなスケッチにしたいのです。

　だから、さっきの見取り図なんてダメですよ。
　あれは、３次元を知っている人間が使うものです。

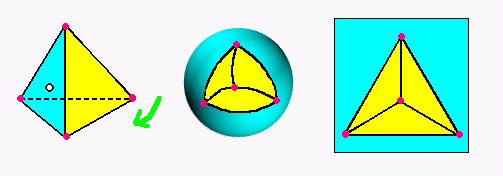
　まずは、正４面体です。

　今度はどれも、いちど球（きゅう）にしてから、１つの面の１点をぬきとって
ぴろ～んってのばせば、スケッチのできあがりです。

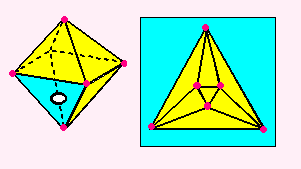
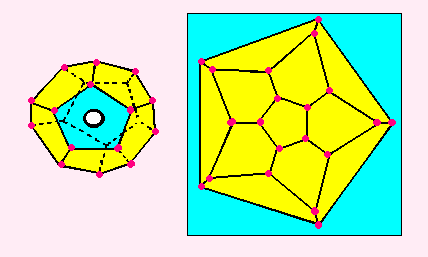
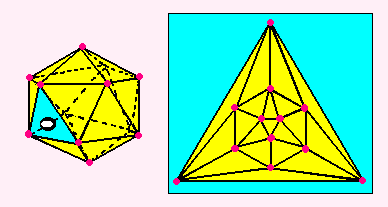
　ほかも、こんなふうになりますね。

　ちなみに、面の個数をかぞえるときは、
まわりの「水色」の面をわすれてはいけませんよ。

　これを使って、
２次元しか知らない人間に、３次元の正多面体をおしえるとどうなるでしょう。

＜２次元の教室にて＞

先生：　「今日は、３次元の正多面体というものをお勉強しますよ。
　　　　　ここから、ず～っと前に進むと、辺にぶつかるわね。
　　　　　そのあと目にした「ふうけい」をおぼえておくのよ。
　　　　　そこからまた、ず～っと前に進むと、また辺にぶつかるわね。
　　　　　そのあと目にした「ふうけい」は、さっきとちょっとちがうでしょ。
　　　　　でも、３次元の正多面体では同じ「ふうけい」が見えるのよ。
　　　　　そこからまたまた、ず～っと前に進むと、またまた辺にぶつかるわね。
　　　　　そのあと目にする「ふうけい」は、さっきとまたちょっとちがうでしょ。
　　　　　でも、３次元の正多面体では同じ「ふうけい」が見えるのよ。
　　　　　そこからまたまた、ず～っと前に進むと、またまた辺にぶつかるわね。
　　　　　そのあと目にする「ふうけい」は、さっきとぜんぜんちがうでしょ。
　　　　　でも、３次元の正多面体では、これが同じ「ふうけい」に見えるの。
　　　　　それに、この２次元の世界では、ここから先へず～っと進んでも、
　　　　　どこまでいっても、もといたところにもどれないでしょ。
　　　　　でも、３次元の世界の正多面体というのはね、
　　　　　なんと、もといたところにもどれるのよ。
　　　　　ず～っと前も、ず～っとうしろも、ず～っとよこの方も、
　　　　　無限（むげん）のかなたで、つながっているって考えるのよ。
　　　　　そして、そのつながってできたところで見える「ふうけい」は、
　　　　　さっきの「ふうけい」と同じなの。」

せいと：　「？？？」

先生：　「それに、この２次元の世界では、「みどり」のところを通らずに、
　　　　　「きいろ」のところへワープしたりできないでしょ。
　　　　　でもね、３次元の世界ではできるのよ。

せいと：　「？？？？？」

●　超立方体　●

　それでは今度は、４次元の超立方体を３次元の空間にスケッチしてみましょう。

　もちろん、３次元しか知らない人間に（ふつうの人はそうですよね～）、
４次元の超立方体ってものをおしえられるようなスケッチにしたいのです。

　・・・とはいっても、
パソコンの画面は平面ですから、３次元の立体を、
（３次元を知っている人ならよくわかる）見取り図を使ってあらわします。

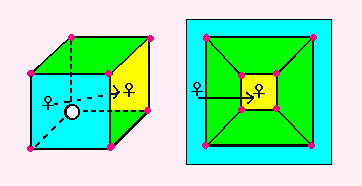
　まずは、立方体をもう一度みてみましょう。

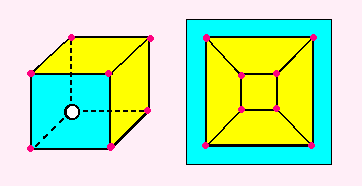
　２次元のスケッチの「みず色」のところを見てください。
　この面が、ちゃんと４本の辺でかこまれているのがみえますね。
　もちろん、「きいろ」の４つの面とのさかいにある辺のことですよ。
　４つの同じ長さの辺でかこまれているのですから、
　りっぱな（？）正方形に、見ようと思えば見えますね。

　超立方体では、立体をとりかこむ空間が、
ちゃんと６つの面でかこまれた立方体に見えればよいだけです。

　それならまさしく、立方体の外がわです。

　そして、その立方体の内がわに、
超立方体ののこりをスケッチすればよいだけです。

　つまり、前は「ななめ」にもちあげた図でしたが、
今度はまわりじゅうにもちあげた（広げた）だけです。

　　今度は、胞つまり立方体の個数をかぞえるとき、
まわりの「水色」の胞（立方体）をわすれてはいけませんよ。

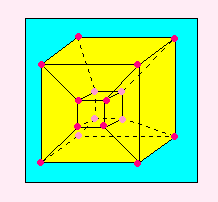
　これを使って、
３次元しか知らない人間に、４次元の超立方体をおしえるとどうなるかって？

　あの～、じつは、わたしも４次元にいったことは・・・

　でも、こんなことはいえそうです。

　もとの立方体の、６つの面からつきでた６つの立方体と、
もともとの立方体と、まわりの「水色」の立方体をあわせると

　　　　　６＋１＋１＝８（個）　の　胞（立方体）

があるけれど、
これって４次元の超立方体ではみんな同じはず。

　だから、超立方体のことを正８胞体っていうのです。

　それから、４次元の世界では、
「水色」の立方体から、「みどり」の立方体のところは通らずに、
「きいろ」の立方体のところへワープできそうです。

●　数える　●

　せっかくですから、超立方体の頂点と辺と面の個数を
数えておきましょう。

　立方体つまり胞の個数が８個ってわかってしまったら、
あとはスケッチをみながらかぞえれば、かんたんです。

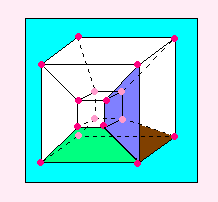
　まず、面は１つの胞（つまり立方体）に６個あります。
　だから、８個の胞だと、６×８＝４８　とはならないで、
どの面も２度ずつかぞえてしまったので２でわります。

　　　　　（６×８）÷２＝２４（個）　・・・　面の個数

　つぎに、辺は１つの面（つまり正方形）に４個あります。
　今度は、どの辺も３度ずつかぞえたことになりますから３でわります。

　　　　　（４×２４）÷３＝３２（個）　・・・　辺の個数

　さいごに、頂点は１つの辺に２個あります。
　今度は、どの頂点も４度ずつかぞえたことになりますから４でわります。

　　　　　（２×３２）÷４＝１６（個）　・・・　頂点の個数

　もちろん（？）、このホームページの「４次元」で出てきた式

　　　　　（頂点）－（辺）＋（面）－（胞）＝０

がなりたっていますね。

HOME（もどる）