平均と平方根

●　いろいろな平均　●

　平均（へいきん）にもいろいろあるって知っていますか。

　身長の平均、体重の平均、テストの点数の平均・・・
という話では、もちろんありません。

　平均するしかたがいろいろあるのです。

●　相加平均　●

　まずは、ふつうに使われる相加平均（そうかへいきん）です。

　「加（か）」　というのは　「加法（かほう）」　で　、たし算のことです。
　相加平均というのは、たし算の平均のことです。

　「わりかん」って知っていますよね。
　これを例にとって考えてみましょう。
　３人で、３００円の物と、５００円の物と、７００円の物を食べたとします。
　みんなで食べたので、わりかんということになりました。
　さて、いくらはらいますか。

　３人とも　□（円）はらうとしましょう。

　　　　□＋□＋□　＝　３００＋５００＋７００　　・・・・・・　(1)

　　　　　　　　□×３　＝　３００＋５００＋７００

　　　　　　　　　　　　　　　３００＋５００＋７００
　　　　　　　　　　^□　＝　　　　　　　３

　　　　　　　　　 　　　＝　５００

　みんな　５００（円）はらうことになりました。

　このように、みんないっしょに　□（円）としたときに、
(1)ように、たし算していっしょにするのを、たし算の平均
つまり、相加平均というのです。
　（ほかの人数でも、どうやって平均するのかわかりますね。）

●　相乗平均　●

　高校になって習うのが相乗平均（そうじょうへいきん）です。

　「乗（じょう）」　というのは　「乗法（じょうほう）」　で　、かけ算のことです。
　相乗平均というのは、かけ算の平均のことです。

　今度は、物価（ぶっか）の上昇（じょうしょう）の例で考えてみましょう。
　最初の１年間で、物価が２倍になりました。
　次の１年間で、物価が４倍になりました。
　その次の１年間で、物価が８倍になりました。
　（大変なインフレです。今はデフレらしいですから、現実ばなれしてますね。）
　さて、１年間につき平均して物価は何倍になったでしょうか。

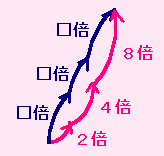
　３年間とも　□倍になったとしましょう。

　　　　□×□×□　＝　２×４×８　　　・・・・・・　(2)

　　　　　　　　　　　　＝　６４

　さて、４×４×４＝６４　ですから、□にあてはまる数は　４　です。

　　　　　　　　　　□　＝　４

　平均して１年間につき物価は４倍になりました。

　このように、どの年もいっしょの　□倍　としたときに、
(2)のように、かけ算していっしょにするのを、かけ算の平均
つまり、相乗平均というのです。
　（ほかの年数でも、どうやって平均するのかわかりますね。）

●　調和平均　●

　今度は、調和平均（ちょうわへいきん）です。

　今度は、仕事にかかる時間の例で考えてみましょう。
　同じ仕事をするのに、それぞれ次の時間かかったとします。

　　　　Aさん　は　　４　（時間）

　　　　Bさん　は　　２　（時間）
　　　　　　　　　　　  _４ 
　　　　^{Cさん　は}　３ 　^{（時間）　　（つまり　８０分）}

　みんな仕事をするスピードがちがうのですね。
　それぞれの仕事をするスピードを、
１時間あたり全体のどれだけすすむかであらわすと

　　　　　　　　　　　  ₁ 
　　　　^{Aさん　は}　4 　^{（／時間）}

　　　　　　　　　　　  _１ 
　　　　^{Bさん　は}　２ 　^{（／時間）}

　　　　　　　　　　　  _３ 
　　　　^{Cさん　は}　４ 　^{（／時間）}

　さて、この仕事の３倍を３人でいっしょにすると何時間かかるでしょうか。

　かかる時間を　□時間　とします。
　そうすると、１時間あたりの仕事のすすむスピードを考えると、次のようになります。

　　  　 １　　　　１　　　　１　　  　１　　　 １　　　　３　
　　　　□　^＋□　^＋□　^＝４　^＋２　^＋４　　　　　^{・・・・・・　(3)}

　　　　　　　　　 １　　　　　　 　１　　　 １　　　　３　
　　　　　　　　　 □　^×３＝ 　４　^＋２　^＋４　

　　　　　　　　　　　　　　　　　　　１　　　 １　　　　３　
　　　　　　　　　　　　１　　　　　　４　^＋２　^＋４
_□^＝　　　　　　　３                

　　　　　　　　　　　　　　　　　　　　　　　　３　　　　　　　　　　　
　　　　　　　　　　　　□　＝　　 １　　　 １　　　　３ 
　　　　　　　　　　　　　　　　　　 ４　^＋２　^＋４　　

　　　　　　　　　　　　　　　　　　　　　　   １　　　 １　　　　３ 
　　　　　　　　　　　　　　　　^{＝　３　÷（} 　４　^＋２　^＋４　^）

　　　　　　　　　　　　　　　　　　　　　　   ６　 
　　　　　　　　　　　　　　　　^{＝　３　÷} 　４　

　　　　　　　　　　　　　　　　＝　２

　けっきょく、２時間　かかることがわかりました。

　このように、みんないっしょの　□時間　としたときに、
(3)のようにしてだした平均を、調和平均というのです。
　（ほかの人数でも、どうやって平均するのかわかりますね。）

●　背理法　●

　どの平均の出し方が一番大きい数になるかというようなお話は、
みなさんが高校生になったら学校でやりますよ。

　今回は、《エラトステネスのふるい》　のじゅんびをしましょう。
　（　《エラトステネスのふるい》　がどんなものかは、また今度のおたのしみ。）

　まずは、相加平均で練習します。本番は相乗平均です。

■　相加平均

　２（人？）の場合で考えます。

　　　　　２　＋　８　＝　５　＋　５　ですから、
　　　　　２　と　８　の　相加平均　は　５　です。
　　　　　このとき　２　は　５　より小さく、　８　は　５　より大きいです。

　　　　　４　＋　６　＝　５　＋　５　ですから、
　　　　　４　と　６　の　相加平均　も　５　です。
　　　　　このとき　４　は　５　より小さく、　６　は　５　より大きいです。

　では、　「　○　と　□　の　相加平均　が　５　のとき、
○　と　□　のどちらかは　５　より小さい。」　といえるでしょうか。

　いえませんね。

　　　　　５　＋　５　＝　５　＋　５　ですから、
　　　　　５　と　５　の　相加平均　も　５　ですが、
　　　　　このとき　５　は　５　と等しく、　５　も　５　と等しいからです。

　こう直しましょう。
　「　○　と　□　の　相加平均　が　５　のとき、
○　と　□　のどちらかは　５　以下である。」　

　なっとくできな〜い！という人には、こう説明するのです。

　だって、もし　○　も　□　も　５　より大きいと
　　　　　　○　＋　□　は　１０　より大きくなって
　　　　　　○　＋　□＝　５　＋　５
と矛盾（むじゅん）するでしょ・・・と。

　このように、もし・・・・ならば矛盾する、という論法を背理法（はいりほう）といいます。
　（もちろん、相加平均が　５　でなくて　他の数でも同じですね。）

■　相乗平均

　今度も、２（年？）の場合で考えます。

　　　　　４　×　９　＝　６　×　６　ですから
　　　　　４　と　９　の　相乗平均　は　６　です。
　　　　　このとき　４　は　６　より小さく、　９　は　６　より大きいです。

　あっ、いけない！

　　　　　４　×　９　＝　（−６）　×　（−６）　ですから
　　　　　４　と　９　の　相乗平均　は　−６　って考える人もいるかも・・・。

　そんなことのないように、これからは正の数で考えることにしましょう。

　続けます。

　　　　　３　×　１２　＝　６　×　６　ですから
　　　　　３　と　１２　の　相乗平均　は　６　です。
　　　　　このとき　３　は　６　より小さく、　１２　は　６　より大きいです。

　さっきと同じように

　　　　　６　×　６　＝　６　×　６　ですから
　　　　　６　と　６　の　相乗平均　は　６　ですが、
　　　　　このとき　６　は　６　と等しく、　６　も　６　と等しいです。

　そこで、こんなことがいえそうです。

　「　○　と　□　の　相乗平均　が　６　のとき、
○　と　□　のどちらかは　６　以下である。」　

　なっとくできな〜い！という人には、背理法で説明してあげてね。
　（もちろん、相乗平均が　６　でなくて　他の数でも同じですね。）

●　開平　●

　ところで、１　と　５　の相乗平均って何ですか。

　　　　　□×□　＝　１×５

　さて、この□にあてはまる数は何でしょう。

　　　　　２×２　＝　４

　ですから、２より大きく、

　　　　　３×３　＝　９

　ですから、３より小さい数です。つまり、
□にあてはまる数は、２より大きく３より小さい数です。

　さあ、□×□　＝　５　となる数を求めてみましょう。
　図でいうと、正方形の一辺の長さを求めることです。

　まず、２×２＝４　だけ正方形にならべます。
　そして、あまった１個を１００等分します。
　大きいのは　１　で、小さいのは　０．０１　です。

　ここまでは、こんなふうに計算します。

　まず、

　　　　　　　　　　　　　　□
　　　　　　　　　□　　　/ ５
　　　　　　　　　□　　　　４　　
　　　　　　　　　○　　　　１００

　ここで、□には　２×２　の　２　が入ります。
　　　　　　５　の下の　４　は　２×２＝４　の　４　です。
　　　　　　その下の　１００　は　あまった１個を１００等分した
　　　　　　０．０１が１００個の　１００　です。

　次に　０．０１を１０ずつかたまりにして（０．０１×１０＝０．１）
これを正方形のまわりにならべます。
　さっき、２×２＝４　だけ正方形にしてならべたので、
そのまわりの　２＋２＝４　ずつならべていきます。

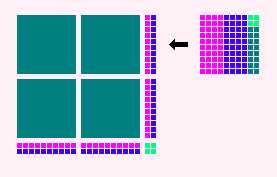
　計算の続きはこうなります。

　　　　　　　　　　　　　　２
　　　　　　　　　２　　　/ ５
　　　　　　　　　２　　　　４　　
　　　　　　　　　４□　　 １００
　　　　　　　　　　□

　ここで、□の中の数は　２列　の　２　です。
　さらに、角のところに　２×２　ならべます。
　０．０１　を　４０×２　と　２×２　のあわせて　８４個　ならべました。

　　　　　　　　　　　　　　２、２□
　　　　　　　　　２　　　/ ５　　　
　　　　　　　　　２　　　　４　　
　　　　　　　　　４２　　  １００
　　　　　　　　　　２　　　　８４　　　
　　　　　　　　　４４□　　　１６００
　　　　　　　　　　　□

　あまった　１６個の　０．０１　を　さらに１００等分して
１６００個の　０．０００１　を正方形のまわりにならべていきます。

　計算の続きはこうなります。

　　　　　　　　　　　　　　２、２３６０６７９
　　　　　　　　　２　　　/ ５　　　
　　　　　　　　　２　　　　４　　
　　　　　　　　　４２　　  １００
　　　　　　　　　　２　　　　８４　　　
　　　　　　　　　４４３　　　１６００
　　　　　　　　　　　３　　　１３２９　　
　　　　　　　　　４４６６　　　２７１００
　　　　　　　　　　　　６　　　２６７９６　　
　　　　　　　　　４４７２０　　　　３０４００
　　　　　　　　　　　　　０　　　　　　　　０　　
　　　　　　　　　４４７２０６　　　３０４００００
　　　　　　　　　　　　　　６　　　２６８３２３６　　
　　　　　　　　　４４７２１２７　　　３５６７６４００
　　　　　　　　　　　　　　　７　　　３１３０４８８９　　
　　　　　　　　　４４７２１３４９　　　４３７１５１１００
　　　　　　　　　　　　　　　　９　　　４０２４９２１４１　　

　いちおう、このへんでやめておくと
けっきょく、□×□　＝　５　となる数は

　　　　□　＝　２．２３６０６７９・・・・・

となることがわかりました。
　じつは、この「・・・・」のところは、けっして同じ数のくりかえし、たとえば

　　　　　　　　　２．２３６０６７９６７９６７９・・・・・

のようにはなりません。
　なぜなら、もし同じ数のくりかえしになると、
＜Q&A＞の「０．９８９８９８・・・・は？」でやったようにして、
分数で書けることになります。そこで

　　　　　　　　　　　　　△　
　　　　　　　　^□　＝　○

とおき、（ただし　△と○は約分しておきます。もちろん○も△も整数です。）
さらに、□×□を計算すると

　　　　　　　　　　　　　　△×△　
　　　　　　^{□×□　＝}　　○×○

　ここで、□×□　＝　５　でしたから、

　　　　　　　　　　　　　　△×△　
　　　^５　＝　 ○×○

　これから、

　　　５×○×○　＝　△×△

となります。ここで、５×○×○は、５で何回われるかを考えると、奇数回です。
　ところが、△×△は、５で何回われるかを考えると、偶数回です。
　（つまり、５×○×○　と　△×△　の素因数分解を考えているのです。）
これって、矛盾してますよね〜。（背理法です）

●　平方根　●

　さて、この　□×□　＝　５　となる数は、

　　　　□　＝　２．２３６０６７９・・・・・

となって、同じ数のくりかえしにならない、つまり循環（じゅんかん）しない
ということがわかりました。

　でも、下の図の正方形の一辺の長さ□を、
いちいち　２．２３６０６７９・・・・・　というのも大変です。

　そこで、□×□　＝　５　の□にあてはまる数を、
正の数と負の数と２つあるので、
正の数の方を　/５　（ルート５）、負の数の方を　−/５　と書いて、
この２つを　５の平方根（へいほうこん）　とよんでいます。

　平方というのは、２乗　のことで、□×□　のように□を２回かけることです。
ついでに、立方というのは　３乗　のことで、□×□×□　のように□を３回かけることです。

　根というのは、方程式の答えのことで、最近は解ということが多いです。
　今の場合は、方程式

　　　　□×□　−５　＝　０

の解（根）のことです。

　いっしょうけんめい求めたことは、次のようになります。

　　　　/５　＝　　２．２３６０６７９・・・・・

　　　　　　　　　（ふじさんろくオームなく・・・・・）
　　　　　　　　　（富士山麓オーム鳴く（泣く？）・・・・・）

　そういえば、そんな名前の宗教団体に泣かされた事件がありましたね。
　これも予言のたぐいだったのかも・・・・・。

HOME（もどる）

掲載内容の無断転載、転用、編集を禁じます。(c) 小林吹代
All Rights Reserved, （c）kobayashi fukiyo , 2001