補数
● 補数って何? ●
10年以上前、こんな質問を受けました。
「補数(ほすう)って何ですか?」
どうも、コンピュータ関係で出てくるらしいのです。
「・・・・・」
ぎゃくに、補数ってどんなものか教えてもらうことになってしまいました。
こういうことでした。
2進法のお話です。
(2進法について知らない人は、
<お勉強>の「1000−1」と「0.999・・・=1」を読んでね。)
たとえば 「0110」 なら こうするというのです。
「1」 と 「0」 を反対にします。
そうすると、「1001」になります。
それに 「1」 をたします。
そうすると 「1010」になります。
このとき、「1010」をもとの「0110」の補数というらしいのです。
それで、なんでこんなことするの?
そもそも、こんなことして出てくる補数って何?
ということでした。
せめてその時、これは負の数をあらわすのに使うんだよ
といってくれたらピンときたと思うのですが・・・。
● 負の数 ●
小学校で習いました。
たし算は入れかえてもいいけど、ひき算は入れかえられない。
2+3 は 3+2 としてもいい
2−3 は 3−2 としてはだめ
これって、とっても不便(ふべん)ですね。
そこで、中学校からはこうなりました。
そのままいれかえてはだめだけど、符号(+や−)をつけてなら入れかえてもいい。
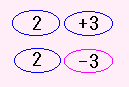
2+3 は +2 と +3 で 入れかえると +3+2
2−3 は +2 と −3 で 入れかえると −3+2
これを使って、こんな計算はかんたんにできました。
![]()
7−4+3−6 = +7+3−4−6
= +10−10
= 0
こうしたのです。
7−4+3−6 は +7 と −4 と +3 と −6 です。
入れかえて プラス と マイナス を集めます。
+7 と +3 を集め −4 と −6 を集めます。
それぞれ計算してから答えをだしました。
それで〜?いったい何がいいたいの?
負の数を作り出したことで、ひき算がたし算になって
とっても便利になったな〜ってことです。
おまけに、5たりない数を −5 ってあらわしたのは、大けっ作!!
ひき算の − と 負の数をあらわす符号の − が同じで、
これをごちゃまぜにして使っていいのですから・・・。
えっ、何一人で感心しているかって?
こういうことです。
5たりない数って、何にたりないかというと、もちろん 0 にです。
そして、 5 に −5 を補(おぎな)うと 0 になります。
5 + (−5) = 0
べつに、ほかのあらわし方をしてもよかったのです。
5 + □ = 0
この □ の数を *5 ってあらわそうが、@5 ってあらわそうが
どうでもよかったのです。
でもこれを −5 ってあらわしたのは すばらしかった!!
と、感心しているのです。
ところで、補集合(ほしゅうごう)って知っていますか。
集合A ではたりないので、補(おぎな)う集合、これが補集合A です。
何にたりないかって?
それは全体集合にです。
集合A に その補集合A を補(おぎな)うと 全体集合 になります。

さて、それでは、補数っていったい何を補(おぎな)っているの?
いったい何にたりないの?
● 0(ゼロ) ●
このホームページのアクセスカウンタをみましたか?
えっ、訪問者が少ないって?
そりゃ、まだ作り始めてから2ヶ月しかたっていないし・・・。
それに、コンテンツが1つ2つしかないうちからUPしてしまったから・・・。
と、苦しい言い訳はどうでもよいとして、
これ 99999 人をオーバーしたらどうなるのでしょう?
99999
+) 1
100000
この 100000 の 1 は オーバーフローしてしまいます。
5けたしか入らないところに 6けたも入れようというのはむりです。
ですから、99999 の次の人は、きっと 00000 になるでしょう。
(そんな日は 永遠にやってこない予定・・・?)
家の方で、車の運転をする人がいたら、聞いてみてください。
走行距離が、10万キロメートルをオーバーすると、どうなるかって・・・。
さて、さんすう・数学では 0 は 0 しかありません。
それも、「0の発見」は大発見(大発明)でした。
でも、コンピュータにとって 0 は 00000 のことで、
100000 も 00000 で やっぱり 0 なのです。
● ひき算 ●
ひき算はとくいですか?
だいたいの人は、きらいですね。
それも、くりさがりのあるひき算は、いやなものです。
今回は、10000円札をだしていくらおつりをもらうか、
つまり、10000 からひく ひき算をやります。
ためしに、 10000−1234 をやってみましょう。
10000
−) 1234
8766
これを、こんなふうにやってみます。
10000 は 9999+1 だから、9999 からひいておいて、後で 1 たすのです。
9999 8765
−) 1234 +) 1
8765 8766
今回は、くりさがりのあるひき算でないので、ちょっぴり楽でしたね。
(でも、あとで 1 たすのをわすれると大変です。)
さて、ここで <お勉強>の「1000−1」 を思い出してください。
10進数では、
10−1=9
100−1=99
1000−1=999
10000−1=9999
2進数では、
(10)2
−(1)2=(1)2
(100)2
−(1)2=(11)2
(1000)2
−(1)2=(111)2
(10000)2
−(1)2=(1111)2
そこで、ためしに (10000)2
−(0110)2
をやってみます。
ただし、今度はとなりから 10 かりてくるのではなく 2 かりてきます。
(10000)2
−) (0110)2
(1010)2
できましたか?
これを、10進数のときと同じようにしてやると、次のようになります。
(1111)2 (1001)2
−) (0110)2 +)
(1)2
(1001)2 (1010)2
ここで、(1111)2 からひくひき算で、
ひいた答えの (1001)2 は、ひく数 (0110)2 の
「1」 と 「0」 を反対にしたもの (1と0の反転)
になっていることに注意してください。
そして、それに 「1」 をたして 答をだしました。
さあ、ここで最初のぎもんにもどりましょう。
こうでしたね。
「0110」 の 補数 はこういうものでした。
「1」 と 「0」 を反対にします。
そうすると、「1001」になります。
それに 「1」 をたします。
そうすると 「1010」になります。
このとき、「1010」をもとの「0110」の補数といいます。
それで、なんでこんなことするの?
そもそも、こんなことして出てくる補数って何?ということでした。
これまでで、(10000)2
−(0110)2 の答えとわかりました。
つまり、
(10000)2 −(0110)2 = (1010)2
さらに、ひき算のたしかめはたし算で・・・ということで、これは
(0110)2 + (1010)2 = (10000)2
となります。
ところが、(10000)2 の 1 は オーバーフローして
じっさいは (0000)2 ですから、けっきょく、次のようになりました。
(0110)2 + (1010)2 = (0000)2
これって、
(0110)2 + □ = (0000)2
の □ にあてはまる数が (1010)2 だということです。
つまり、負の数です。
(0110)2 は 6 ですから、 −6 にあたる数が (1010)2 だということです。
● 整数 ●
2進法で、正の整数と負の整数をあらわしてみましょう。
お話を 4けた ですすめましょう。
10進法の 0 は 2進法の (0000)2
10進法の 1 は 2進法の (0001)2
10進法の 2 は 2進法の (0010)2
10進法の 3 は 2進法の (0011)2
10進法の 4 は 2進法の (0100)2
10進法の 5 は 2進法の (0101)2
10進法の 6 は 2進法の (0110)2
10進法の 7 は 2進法の (0111)2
今度は、負の数です。
10進法の −1 は 2進法の (0001)2 の補数で (1111)2
【求め方】 (0001)2 −−> (1110)2 −−> (1111)2
10進法の −2 は 2進法の (0010)2 の補数で (1110)2
【求め方】 (0010)2 −−> (1101)2 −−> (1110)2
10進法の −3 は 2進法の (0011)2 の補数で (1101)2
【求め方】 (0011)2 −−> (1100)2 −−> (1101)2
10進法の −4 は 2進法の (0100)2 の補数で (1100)2
【求め方】 (0100)2 −−> (1011)2 −−> (1100)2
10進法の −5 は 2進法の (0101)2 の補数で (1011)2
【求め方】 (0101)2 −−> (1010)2 −−> (1011)2
10進法の −6 は 2進法の (0110)2 の補数で (1010)2
【求め方】 (0110)2 −−> (1001)2 −−> (1010)2
10進法の −7 は 2進法の (0111)2 の補数で (1001)2
【求め方】 (0111)2 −−> (1000)2 −−> (1001)2
もう一度まとめましょう。(4けたであらわす場合です。)
0 は (0000)2
1 は (0001)2 −1 は (1111)2
2 は (0010)2 −2 は (1110)2
3 は (0011)2 −3 は (1101)2
4 は (0100)2 −4 は (1100)2
5 は (0101)2 −5 は (1011)2
6 は (0110)2 −6 は (1010)2
7 は (0111)2 −7 は (1001)2
さて、4けたであらわせる数がもうひとつあります。
そう、(1000)2 です。
これは何にしたらよいでしょうか。
一番上の位の数が 1 ですから、負の数です。
そして、111、110、101、100、011、010、001 の次ですから・・・。
そうですね。
−7 の もうひとつ下 つまり −8 にするとよさそうです。
そうすると、4けたで整数をあらわそうとすると、
−8 から +7 まで
の数があらわせます。
プログラムをくむとき、変数という入れ物を使います。
そして、その変数という入れ物には、大きさだけでなく、
中に入れる数によって、いろいろな種類(型)があります。
正の整数だけを入れるとか、(正負の)整数を入れるとか、小数を入れるとか・・・。
(正負の)整数を入れる変数の型で、
マイナスいくらからプラスいくらまでの数を入れられるのか、
一度じっくり見てみてください。
たとえば、C言語では次のようになっています。
char は 8けたで −128 〜 +127
short は 16けたで −32768 〜 +32767
long は 32けたで −2147483648 〜 +2147483647
+と−の後に続く数(絶対値)が 1 ちがっていますね。
(あまりにも、こまかい話ですが・・・)
最後に、コンピュータは、ひき算はたし算でやるのです。
もう、どうするのかわかった人もいますね。
できたら、また今度お話するかも・・・。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001