双曲幾何（１）

●　次元　●

　このホームページで「４次元」のお話をしました。

　そうしたら、こんなメールをいただきました。

　この世界は「４次元」ですよ！
　・・・・・・
　・・・というわけで、時間を入れるのです。
　・・・・・・。

　きっと、アインシュタインの
相対性理論（そうたいせいりろん）のことをいいたかったのでしょうね。

　ざんねんながら、前回やったのは、
４次元は４次元でも、「４次元のユークリッド空間」のお話でした。

　だから、相対性理論とは、ぜ〜んぜん関係（かんけい）ありません。

　ユークリッド空間って・・・？

　おおざっぱにいうと、「まがっていない、まっすぐな空間」のことです。

　・・・ということは？

　そう！

　「まっすぐでない、まがった空間」だって考えられるということです。

　では、前回とおなじように、みていきましょう。

＜　０次元　＞

　まずは、０次元です。
　点です。

　　　　　●

　・・・とりたてて、何もいうことはありません。

＜　１次元　＞

　次は、１次元です。
　直線・・・とは、かぎりませんね。

　そう、曲線（きょくせん）かもしれません。

　円とか、放物線（ほうぶつせん）とか、ぐにゃぐにゃの名前もない曲線とか・・・

＜　２次元　＞

　次は、２次元です。
　平面・・・とは、かぎりませんね。

　そう、曲面（きょくめん）かもしれません。

　球（の表面）とか、円柱（の側面）とか、山あり谷ありの名前もない曲面とか・・・

＜　３次元　＞

　次は、３次元です。
　空間・・・とは、かぎりま・・・

　（さあ、なんといったらよいものやら）

　ぐにゃぐにゃに曲がった３次元の空間って、さてどんなものなのでしょう。

　４次元どころか、３次元でも・・・

　？？？・・・・・！

●　正多面体　●

　このホームページでの「正多面体」で、こんなことをやりました。

　正多面体が５種類、つまり

しかないことを、正３角形、正４角形（正方形）、正５角形を、
じっさいにはりあわせて、たしかめてみました。

　そこでは・・・

＜正３角形＞

　１つの頂点（ちょうてん）のまわりに、
正３角形を３枚、４枚、５枚使ってできる正多面体をみたあとで、
６枚の場合に、こんなことをいいましたね。

　ここでやめておけばいいものを、さらには

　「もちろん、７枚以上使ったら、ぺったんこどころか重なってしまいますね。」なんて・・・。

　でも、正多面体を作るつもりがないのなら、話はべつです。

　１つの頂点（ちょうてん）のまわりに、７枚（以上）の正３角形をはりあわせていって、
どんどん「でこぼこの平面（曲面？）」を作っていけます。

　ぜひいちど作ってみてください。

　本当は、ここにその作品の写真をのせたかったのですが、
あまりにも出来ばえが・・・。
　（かといって、図にするのもむずかしくて・・・）

＜正５角形＞

　さて、工作をするにも、図にかくにも
手ごろなのは正５角形を使ったものです。

　ですから、正４角形（正方形）はとばして、
正５角形をみてみることにしましょう。

　また、１つの頂点のまわりに何枚使うかで考えていって、
１つの頂点のまわりに３枚使ってできるのが、正１２面体でした。

　ここでやめておけばいいものを、さらにはまたまた

　「４枚以上使ったら、ぺったんこどころか重なってしまってできませんね。」なんて・・・。

　でも、またしても正多面体を作るつもりがないのなら、話はべつです。

　１つの頂点（ちょうてん）のまわりに、４枚（以上）の正５角形をはりあわせていって、
どんどん「でこぼこの平面（曲面？）」を作っていけます。

　これもまた、ぜひいちど作ってみてください。（おすすめです！）

　本当は、ここにその作品の写真をのせたかったのですが、
またしても、あまりにも出来ばえが・・・。

　でも、図ならなんとか・・・（といっても、１つの頂点のまわりの４枚だけですが）

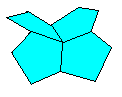
　さあ、こんな形の（もっとなめらかな）ものを知っていますか。

　そう、馬に乗るときに使う鞍（くら）の形ににていますね。

＜正６角形＞

　次に正６角形を使ってできる正多面体をみていきましょうということで、
１つの頂点のまわりに３枚使って・・・というところで、
はやくもむりとなってしまいましたね。

　でも、またしても正多面体を作るつもりがないのなら、話はべつです。

　１つの頂点（ちょうてん）のまわりに、４枚（以上）の正６角形をはりあわせていって、
どんどん「でこぼこの平面（曲面？）」を作っていけます。

　「もちろん、正７角形からさきも、さいしょからむりというものです。」・・・
なんてこともありません。

　正７角形だって、正多面体を作るつもりがないのなら、へっちゃらです。

●　タイルばり　●

　「ペンローズ・タイル」というのを、このホームページでもとりあげましたね。

　そうそう、ペンローズというのは、
ペンタグラムのローズ（バラの花）なんかじゃなくって、
人の名前でした。

　その人は、正５角形で「タイルばり」しようとすると、
どうしてもすきまができてしまうことから、
２種類（しゅるい）のタイルを発明（？）して、
無限（むげん）に広がる平面を「タイルばり」してみせたのです。

　でも、正５角形を使って、まっすぐに広がる平面を「タイルばり」するのはむりでも、
曲面ならば・・・だいじょうぶ、だいじょうぶ！

　そう思って見てみると・・・

　これらの正多面体だって、中に空気を入れてふくらませて球にすれば・・・

　正３角形や正４角形（正方形）や正５角形で、
ちゃ〜んと球（の表面）を「タイルばり」していますね。

　えっ、そんなことしたら辺がカーブしてしまうって？

　気にしない！気にしない！

　球（の表面）に住んでいる人には、
それが直線だってお約束すればいいのですから。

　「タイルばり」するのが平面でなくって、
球（の表面）のように、ほかのものでもいいのなら・・・

　さっきやったように、１つの頂点（ちょうてん）のまわりに、
４枚（以上）の正５角形をはりあわせていって、
どんどん作っていった「でこぼこの平面（曲面？）」だって、
ちゃ〜んと正５角形で「タイルばり」されています。

　えっ、そんなのあたりまえだ〜って？

HOME（もどる）

掲載内容の無断転載、転用、編集を禁じます。(c) 小林吹代
All Rights Reserved, （c）kobayashi fukiyo , 2001