二項分布

二項分布

●　パスカルの三角形　●

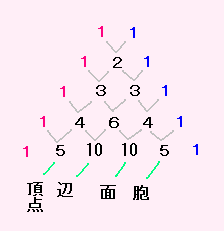
　パスカルの三角形って、こんな三角形でした。

　　　　　　　　　　　　　　　　　　　　　　　　　　　１
　　　　　　　　　　　　　　　　　　　　　　　　　１　　　１
　　　　　　　　　　　　　　　　　　　　　　　１　　　２　　　１
　　　　　　　　　　　　　　　　　　　　　１　　　３　　　３　　　１
　　　　　　　　　　　　　　　　　　　１　　　４　　　６　　　４　　　１
　　　　　　　　　　　　　　　　　１　　　５　　１０　　１０　　　５　　　１

　これは、１次元、２次元、３次元、４次元・・・の三角形の
頂点や辺の個数としてあらわれましたね。
　（くわしくは、このホームページの「４次元」を見てね。）

　そして、２項定理でこれらの数が出てきました。

　　（ａ＋ｂ）^０　＝　１

　　（ａ＋ｂ）^１　＝　１ａ　＋　１ｂ

　　（ａ＋ｂ）^２　＝　１ａ^２　＋　２ａｂ　＋　１ｂ^２　

　　（ａ＋ｂ）^３　＝　１ａ^３　＋　３ａ^２ｂ　　＋　３ａｂ^２　＋　１ｂ^３　

　　（ａ＋ｂ）^４　＝　１ａ^４　＋　４ａ^３ｂ　＋　６ａ^２ｂ^２　＋　４ａｂ^３　＋　１ｂ^４　

　　（ａ＋ｂ）^５　＝　１ａ^５　＋　５ａ^４ｂ　＋　１０ａ^３ｂ^２　＋　１０ａ^２ｂ^３　＋　５ａｂ^４　＋　１ｂ^５　

　ところで、パスカル自身はこの三角形を何に使っていたか知っていますか。

　じつは、確率（かくりつ）に使っていたそうです。

　この三角形じたいは、古くから知られていたのですが、
パスカルが確率の研究で、さかんに使ったことから、
「パスカルの三角形」とよばれるようになったとのことです。

　さて、　ａ　か　ｂ　のどちらかがおきるといえば　・・・
　ａ　を「表（おもて）がでる」で　ｂ　を「裏（うら）がでる」って思うと　・・・
　そう、「コインなげ」ですね。

　このホームページの「パスカルの三角形」でやったように

　　　　　ａ　というのを　道で上にいくこと
　　　　　ｂ　というのを　道で横にいくこと

というようにしたければ、コインをなげて、
「表」か「裏」かで、上にいくか横にいくかきめればいいってものです。

●　二項分布　Ｂ（ｎ，1/2）　●

　「コインなげ」を１回したら・・・「表がでる（ａ）」か「裏がでる（ｂ）」です。

　　（ｂ＋ａ）^１　＝　１ｂ　＋　１ａ

　どうして、ａ　と　ｂ　をいれかえたかって？

　　　　　「裏がでる（ｂ）」ってことは、「表のでる枚数」が　０　枚
　　　　　「表がでる（ａ）」ってことは、「表のでる枚数」が　１　枚

ってことで、数におきかえるなら、（それが算数・数学ってものです！？）
やっぱり、小さいじゅんでないとね。

　つまりは、ａについて「昇べきのじゅん」にならべかえただけです。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　１
　さて、ここで「表がでる（ａ）」確率も「裏がでる（ｂ）」確率も　----　ですから
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２

　　　　１　　　　　１　　　　　１　　　　　１
　　（----　＋　----）＝　----　＋　----
　　　　２　　　　　２　　　　　２　　　　　２

　　　　　　　　　　　　　　　　１　　　　　１
　　　　　　　　　　　１　＝　----　＋　----
　　　　　　　　　　　　　　　　２　　　　　２

　では、「コインなげ」を２回したら・・・

　　　　　「２回とも裏（ｂ^２）」　　　　つまり　「表の枚数」が　０　枚
　　　　　「１回表で１回裏（ａｂ）」　つまり　「表の枚数」が　１　枚
　　　　　「２回とも表（ａ^２）」　　　　つまり　「表の枚数」が　２　枚

のどれかです。

　　（ｂ＋ａ）^２　＝　１ｂ^２　＋　２ａｂ　＋　１ａ^２　

　　　　　　　　　１　　　　　　　１
　ここで、ａ＝----　，　ｂ＝----　とすると
　　　　　　　　　２　　　　　　　２

　　　　　　　　　　　　１　　　　　　２　　　　　１
　　　　　　　１　＝　----　＋　----　＋　----
　　　　　　　　　　　　４　　　　　　４　　　　　４

　こんなちょうしで、パスカルの三角形

から、「コインなげ」の確率ができあがります。

　　　　　　　　　　　　　　　　　　　　　　　　　　　１

　　　　　　　　　　　　　　　　　　　　　　　　　１　　　１
　　　　　　　　　　　　　　　　　　　　　　　　----　　----
　　　　　　　　　　　　　　　　　　　　　　　　　２　　　　２

　　　　　　　　　　　　　　　　　　　　　　　１　　　２　　　１
　　　　　　　　　　　　　　　　　　　　　　----　----　----
　　　　　　　　　　　　　　　　　　　　　　　４　　　４　　　４

　　　　　　　　　　　　　　　　　　　　　１　　　３　　　３　　　１
　　　　　　　　　　　　　　　　　　　　----　----　----　----
　　　　　　　　　　　　　　　　　　　　　８　　　８　　　８　　　８

　　　　　　　　　　　　　　　　　　　１　　　４　　　６　　　４　　　１
　　　　　　　　　　　　　　　　　　----　----　----　----　----
　　　　　　　　　　　　　　　　　　１６　　１６　　１６　　１６　　１６

　　　　　　　　　　　　　　　　　１　　　５　　１０　　１０　　　５　　　１
　　　　　　　　　　　　　　　　----　----　----　----　----　----
　　　　　　　　　　　　　　　　３２　　３２　　３２　　３２　　３２　　３２

　この表から、たとえば、「コインなげ」を４回するのなら・・・

　　（ｂ＋ａ）^４　＝　１ｂ^４　＋　４ｂ^３ａ　＋　６ｂ^２ａ^２　＋　４ｂａ^３　＋　１ａ^４　・・・　（１）

　　　　　「４回とも裏（ｂ^４）」　　　　　　つまり　「表の枚数」が　０　枚
　　　　　「１回表で３回裏（ａｂ^３）」　　つまり　「表の枚数」が　１　枚
　　　　　「２回表で２回裏（ａ^２ｂ^２）」　つまり　「表の枚数」が　２　枚
　　　　　「３回表で１回裏（ａ^３ｂ）」　　つまり　「表の枚数」が　３　枚
　　　　　「４回とも表（ａ^４）」　　　　　　つまり　「表の枚数」が　４　枚

のどれかがおきて、

　その確率は、それぞれ

となります。そして、これらをぜんぶたし算すると

　　　　　　　　　１　　　　　　　１
　（１）で、ａ＝----　，　ｂ＝----　とすれば
　　　　　　　　　２　　　　　　　２

　　　　　　　１　　　１　^４　　　　１　　　４　　　　６　　　４　　　１
　　　　　（----＋----）　＝　----＋----＋----＋----＋----
　　　　　　　２　　　２　　　　　１６　　１６　　１６　　１６　　１６

　　　　　　　　　１　　　４　　　　６　　　４　　　１
　　　　　１＝　----＋----＋----＋----＋----　
　　　　　　　　　　　　　　　　　１６　　１６　　１６　　１６　　１６

　そう、ちゃ～んと確率「１」つまり「１００％」になっています。
　（これらのうち、どれかがおきるということですね。）

●　二項分布　Ｂ（ｎ，1/3）　●

　今度は、「さいころなげ」を１回したら・・・

　「１の目」か「２の目」か「３の目」か「４の目」か「５の目」か「６の目」がでます。

　でも、６通りのどれがおきるかってことはやめておいて、
「Ａ」　か　「Ｂ（Ａでない）」　か、って考えられるものだけにしましょう。

　たとえば、

　　　　　「１の目がでる」　か　それとも　「１以外の目がでる」　か
　　　　　「偶数の目がでる」　か　それとも　「奇数の目がでる」　か
　　　　　「３の倍数の目がでる」　か　それとも　「それ以外の目がでる」　か

といったものです。

　このうち、今回は

　　　　　「３の倍数の目がでる（ａ）」　か　「それ以外の目がでる（ｂ）」　か

を考えてみましょう。

　　（ｂ＋ａ）^１　＝　１ｂ　＋　１ａ

　　　　　「それ以外の目がでる（ｂ）」ってことは、「３の倍数の目がでる回数」が　０　回
　　　　　「３の倍数の目がでる（ａ）」ってことは、「３の倍数の目がでる回数」が　１　回

　今度は

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　１
　　　　　「３の倍数の目がでる（ａ）」　確率　は　　----　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　３

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２
　　　　　「それ以外の目がでる（ｂ）」　確率　は　　----　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　３

ですから、

　　　　２　　　　　１　　　　　２　　　　　１
　　（----　＋　----）＝　----　＋　----
　　　　３　　　　　３　　　　　３　　　　　３

　　　　　　　　　　　　　　　　２　　　　　１
　　　　　　　　　　　１　＝　----　＋　----
　　　　　　　　　　　　　　　　３　　　　　３

　では、「さいころなげ」を２回したら・・・

　　「２回ともそれ以外（ｂ^２）」　　　　　　　　つまり　「３の倍数の回数」が　０　回
　　「１回３の倍数で１回それ以外（ａｂ）」　つまり　「３の倍数の回数」が　１　回
　　「２回とも３の倍数（ａ^２）」　　　　　　　　つまり　「３の倍数の回数」が　２　回

のどれかです。

　　（ｂ＋ａ）^２　＝　１ｂ^２　＋　２ａｂ　＋　１ａ^２　

　　　　　　　　　１　　　　　　　２
　ここで、ａ＝----　，　ｂ＝----　とすると
　　　　　　　　　３　　　　　　　３

　　　　　　　　　　　　４　　　　　　４　　　　　１
　　　　　　　１　＝　----　＋　----　＋　----
　　　　　　　　　　　　９　　　　　　９　　　　　９

　こんなちょうしで、今度はパスカル風三角形

　　　　　　　　　　　　　　　　　　　　　　　　　　　１
　　　　　　　　　　　　　　　　　　　　　　　　　２　　　１
　　　　　　　　　　　　　　　　　　　　　　　４　　　４　　　１
　　　　　　　　　　　　　　　　　　　　　８　　　12　　　６　　　１
　　　　　　　　　　　　　　　　　　　16　　　32　　　24　　　８　　　１

から、「さいころなげ」の（３の倍数の）確率がでてきそうです。

　ちなみに、　パスカル風三角形というのは、
１次元、２次元、３次元、４次元・・・の正方形の
頂点や辺の個数としてあらわれましたね。
　（くわしくは、このホームページの「多項定理」を見てね。）

　さあ、確率はこうなります。

　　　　　　　　　　　　　　　　　　　　　　　　　　　１

　　　　　　　　　　　　　　　　　　　　　　　　　２　　　１
　　　　　　　　　　　　　　　　　　　　　　　　----　　----
　　　　　　　　　　　　　　　　　　　　　　　　　３　　　　３

　　　　　　　　　　　　　　　　　　　　　　　４　　　４　　　１
　　　　　　　　　　　　　　　　　　　　　　----　----　----
　　　　　　　　　　　　　　　　　　　　　　　９　　　９　　　９

　　　　　　　　　　　　　　　　　　　　　８　　　１２　　　６　　　１
　　　　　　　　　　　　　　　　　　　　----　　----　----　----
　　　　　　　　　　　　　　　　　　　　　２７　　２７　　２７　　２７

　　　　　　　　　　　　　　　　　　　１６　　３２　　２４　　８　　　１
　　　　　　　　　　　　　　　　　　----　----　----　----　----
　　　　　　　　　　　　　　　　　　８１　　８１　　８１　　８１　　８１

●　標準化　●

　　１次元、２次元、３次元、４次元・・・の三角形や正方形の
頂点や辺の個数が、ず～っと高い次元では何個ぐらいになるか・・・
なんて、だ～れもきょうみないってものです。

　おそらく、きょうみのない確率は、
かぎりなく　１　（１００％）に近いでしょう。

　ところが、ギャンブル（かけごと）となると話はべつです。

　ず～っと、負けっぱなし・・・。
　これって、ちょっとへんじゃないかな～。
　いったいぜんたい、そんなに負ける確率って、どれくらいなんだろう。
　がぜん、きょうみがわいてくるってものです。

　つまり、回数が多いときはどうなるかってことです。
　（図形なら、ず～っと高い次元ではどうなるかってことです。）

　まずは、「コインなげ」と「さいころなげ」をグラフにしてみましょう。

　もちろん「たてじく」には確率をとるとして、
「よこじく」には何をとるといいでしょうか。

　まってました、といわんばかりですね。

　　　　　「表のでる枚数」が　０　枚
　　　　　「表のでる枚数」が　１　枚

というように、数におきかえておいてよかったというものです。
　それも、小さいじゅんの・・・。

　「コインなげ」はこうなります。

＜　コインなげ　＞

　「さいころなげ」はこうなります。

＜　さいころなげ　＞

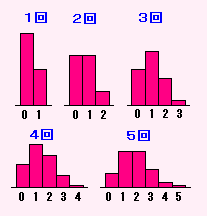
　さて、このまま回数をふやしても
横に長くて、たてにみじかい、べた～っとしたグラフになるだけです。

　そこで、「よこじく」には何をとるかということにもどって、
ちょっとそこの数にかけ算をして、のびちぢみさせたり、
ひき算をして、ずらしたりするのです。

　さらに、「たてじく」の方も、ぜんぶの面積が１になるように
ちょっとのびちぢみさせるのです。

　そうすると、こうなります。

＜　コインなげ　＞

＜　さいころなげ　＞

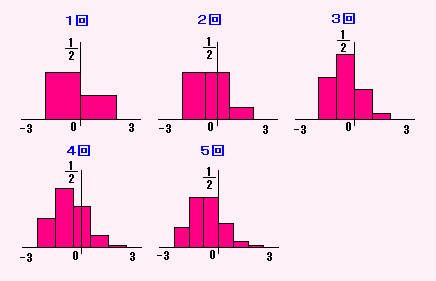
●　正規分布　●

　さっきの「コインなげ」や「さいころなげ」の回数を、う～んとふやすと、
のびちぢみさせた方のグラフはどうなるでしょうか。

　なんと、どちらも同じグラフに近づいていくというのです。

　「コインなげ」は

　　　　　　　　　１　　　　　　　１
　　　　　　ａ＝----　，　ｂ＝----　
　　　　　　　　　２　　　　　　　２

だったし、「さいころなげ」は

　　　　　　　　　１　　　　　　　２
　　　　　　ａ＝----　，　ｂ＝----　
　　　　　　　　　３　　　　　　　３

だったので、

　　　　　「パスカルの三角形」　と　「パスカル風三角形」

ていどのちがいがでてきました。

　つまり、

　　　　　「パスカルの三角形」は、左右対称（たいしょう）でしたが、
　　　　　「パスカル風三角形」は、ちょっとね～といったものでした。

　それが、回数をふやすと、どちらもこんなグラフになるというのです。

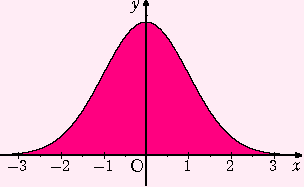
　これは、（標準）正規分布（せいきぶんぷ）とよばれているものです。

　ということは・・・

　「パスカル風三角形」だって、
そのうち左右対称に近いものになっていくってことです。

　ということは、さらに・・・

　１次元、２次元、３次元、４次元・・・っていってるうちは、

　　　　　「三角形」　と　「正方形」

の頂点や辺の個数なんて、バラバラなように思うけど、

　な～に、う～んと高い次元では、
にたような「わりあい」であらわれてきて、

　しかも、考えている次元の半分ぐらいの胞のようなものが、
だんぜん個数が多いってことになりますね。

HOME（もどる）