パスカルの三角形
● 和の法則 ●
まわり道しないで、左下から右上までいく道順(みちじゅん)は何通り?
そう、6通りですね。
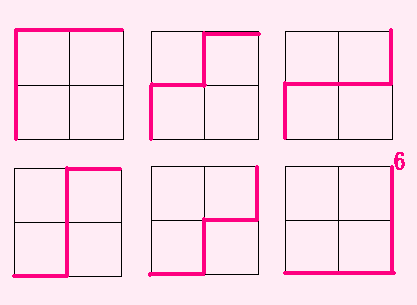
では、下の図では何通りかな?
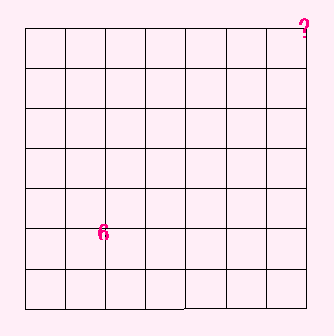
高校生なら、ワンパターンで(?)パッと答えをだすかもしれませんね。
でも、こんなの小学生だってできるのです。
といっても、ちょくせつ数えるのはたいへんです。
そういうときは、ちょっとかんたんな場合でやってみるのです。
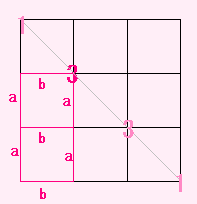
下の図で、? は何通りかと考えてみます。
6 というのは、そこまでいく道順は6通りということで、
これはさっきやりましたね。
4 というのも数えてあったとしましょう。
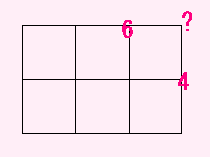
そうすると、? に行くには、どちらかを通らないといけませんから、
(左から右へ行く)こんな図と同じことですね。
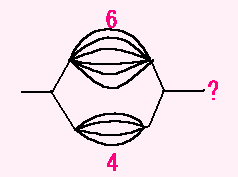
これなら、
6+4=10
で、あわせて 10通り です。
たし算の答えのことを和(わ)というので、和の法則とよばれています。
そうすると、左下の 1 から どんどんたしていけば、
数えまちがわずに(たし算をまちがえなければ)答えがでますね。
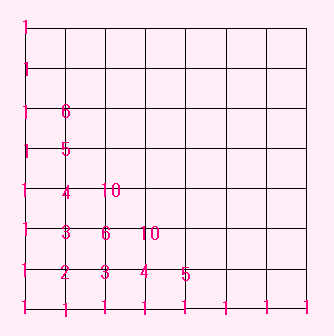
どうなりましたか。
ちゃんと、3432通り とでましたか。
(高校ではもっとうまく数える方法を勉強しますよ。)
さて、この表のななめの数をたしてみましょう。
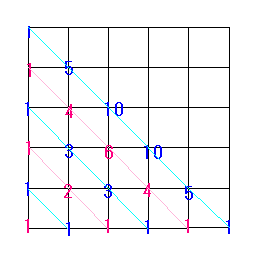
1=20
1+1=21
1+2+1=22
1+3+3+1=23
1+4+6+4+1=24
1+5+10+10+5+1=25
いつも、2を何回かかけた数になっています。
こうなるわけがわかりますか。
それは、たとえば
1+3+3+1=23
というのは、(小さい正方形の一辺を1歩とすれば)
3歩でいけるところを数えているだけなのです。
それは、図でいうと 1,3,3,1 のところに行く方法ですから、
1+3+3+1 (通り)
でも、1歩ごとに上へ行こうか右に行こうかと考えれば
2×2×2=23 (通り)
となるからです。
こちらは、かけ算の答えのことを積(せき)というので、積の法則とよばれています。
● パスカルの三角形 ●
いままで考えてきた道順の数(とその出し方)は、
パスカルの三角形として、とっても有名です。
ただし、三角形というくらいですから、(このままではパスカルの正方形!?)
ちょっと回転(かいてん)させるのです。
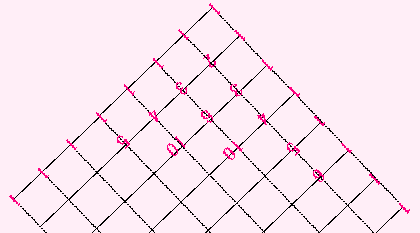
では、パスカルの三角形をきちんとかいてみましょう。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
さて、2項定理でこれらの数が出てくるのが、とっても有名です。
こんなことでしたね。
(a+b)0 = 1
(a+b)1 = 1a + 1b
(a+b)2 = 1a2 + 2ab + 1b2
(a+b)3 = 1a3 + 3a2b + 3ab2 + 1b3
(a+b)4 = 1a4 + 4a3b + 6a2b2 + 4ab3 + 1b4
(a+b)5 = 1a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + 1b5
では、どうしてこんなところに道順の数がでてくるのでしょうか。
(a+b)3 = 1a3 + 3a2b + 3ab2 + 1b3
で、みていくことにしましょう。
(a+b)3 = (a+b)(a+b)(a+b)
これを展開(てんかい)すると、
それぞれの「かっこ」の中からaかbを取り出してきて、かけたものが出てきます。
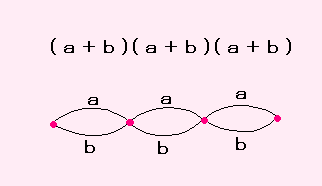
ですから、たとえば a2b なら、
(a+b)(a+b)(a+b) の aab は a2b
(a+b)(a+b)(a+b) の aba も a2b
(a+b)(a+b)(a+b) の baa も a2b
となって、全部で 3a2b が出てきます。
これを、パスカルの三角形(正方形!?)に翻訳(ほんやく)するのに、
a というのを 道で上にいくこと
b というのを 道で横にいくこと
と考えると、
(a+b)(a+b)(a+b)
というのは、1歩ごとに上へ行こうか右に行こうかと考えながら3歩いくことになります。
そこでは、さっきの a2b というのは、上に2歩、横に1歩で行く道順で、
具体的には
aab ,aba ,baa
の3通りということになります。
さっきは、かけ算の順番を入れかえるとどれも a2b になって、
この3つで3a2b が出てきました。
今度は、この3通りのどの行き方も着いた所が同じ場所で、
そこに 3 と書きこんだのです。
この3通りの 3 などを書きならべたのがパスカルの三角形ですから、
二項定理そのものということになるのですね。
● フィボナッチ数 ●
今度は、傾き(かたむき)をちょっとかえたななめの数をたしてみましょう。
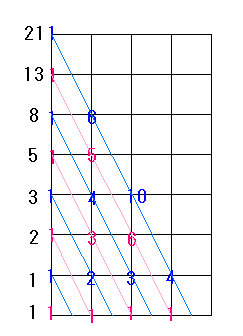
1
1
1+1=2
1+2=3
1+3+1=5
1+4+3=8
1+5+6+1=13
1+6+10+4=21
おぼえていますか。
1,1,2,3,5,8,13,21
これは、<お勉強>の「黄金数」や「フィボナッチ数」でやった
フィボナッチ数ですね。
フィボナッチ数が、このパスカルの三角形(正方形!?)に出てくることは
よく知られています。
図をたどっていくと、
(1以外は)1つ1つが前の数とその前の数をあわせた数になっているのだから
これらをあわせたって、そうなるなって読みとれますね。
前の数とその前の数をあわせた数というと、
そう、フィボナッチ数です。
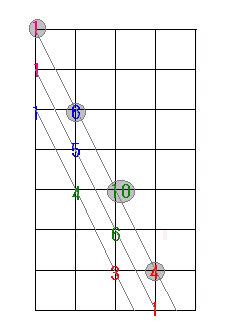
いちおう計算でたしかめて(?)おきましょう。
(べつに分数の分子を見なくても、その横の筆算だけでいいのですが・・・)
1 1+1
1+-- = ------
1 1
1 1+2 1+1
1+------ = -------- ここで +) 1
1+1 1+1 1+2
1+1 1+3+1 1+2
1+------ = -------- ここで +) 1+1
1+2 1+2 1+3+1
1+2 1+4+3 1+3+1
1+-------- = -------- ここで +) 1+2
1+3+1 1+3+1 1+4+3
1+3+1 1+5+6+1 1+4+3
1+-------- =------------ ここで +) 1+3+1
1+4+3 1+4+3 1+5+6+1
1+4+3 1+6+10+4 1+5+6+1
1+------------ =-------------- ここで +) 1+4+3
1+5+6+1 1+5+6+1 1+6+10+4
● 「階段登り」と「畳敷き」 ●
さて、計算はこのへんにして、
このことを利用したフィボナッチ数の例を紹介(しょうかい)しましょう。
まえにやった
1+3+3+1=23
というのは、(小さい正方形の一辺を1歩とすれば)
3歩でいけるところを数えたのでした。

それなら、
1+3+1=5 (ここで 5はフィボナッチ数)
は、何を数えているのでしょうか。
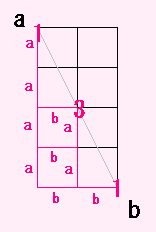
aaaa だと 上に4歩ですが、
aab だと 上に2歩、横に1歩で あわせて 3歩
bb だと 横にたったの 2歩 です。
でも、もし bの1歩 が aaの2歩 と同じと考えられるようなときには、
aaaa は 4歩ですが、
aab も bがaaと同じなら あわせて 4歩
bb も bがaaと同じなら あわせて 4歩 です。
それなら、bの1歩 が aaの2歩 と同じと考えられるようなものには、
どんなものがあるでしょうか。
そのような例として有名なものに
「階段登り(かいだんのぼり)」と「畳敷き(たたみしき)」があります。
<階段登り>
階段(かいだん)を、1度に1段か2段で上がる方法は何通り?
といった問題です。
下の図は4段の階段を上がる方法です。
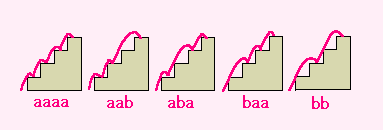
1度に2段上がることを b とすれば、
それは1度に1段上がるのを a としたときの aa と同じと考えられますから、
まさしくこの例にぴったりです。
(ただし、0段の階段を登る方法は 1通り ということにします。)
0段 は 1通り
1段 は 1通り
2段 は 2通り
3段 は 3通り
4段 は 5通り
といったように フィボナッチ数が出てきます。
<畳敷き>
昔は間口の広さにおうじて税金(ぜいきん)がかけられたそうで、
細長い家が多かったとのことです。
それとは、何の関係もないのですが
たたみ1畳の長い方のはばで、どんどん畳(たたみ)をしいていきましょう。
そうしたら、畳のしき方は何通り?
といった問題です。
下の図は、畳の短い方で 4枚分 の長さになったときのしき方です。
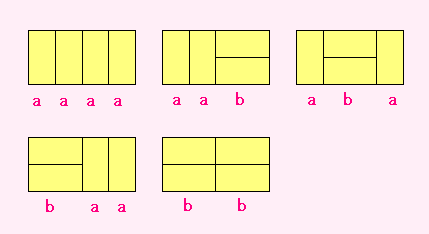
横にしてしくのを b とすれば、
それはたてにしてしくのを a としたときの aa と同じ長さだけ横にのびますから、
まさしくこの例にぴったりです。
(ただし、畳の短い方で0枚分の長さのときのしき方は 1通り ということにします。)
0枚分 は 1通り
1枚分 は 1通り
2枚分 は 2通り
3枚分 は 3通り
4枚分 は 5通り
といったように フィボナッチ数が出てきます。
フィボナッチ数は、自然の中にいっぱい見られるそうですが、
今回はずいぶんと人工的な例になってしまいました。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001