ペル方程式
● ペル方程式 ●
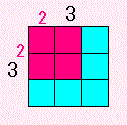
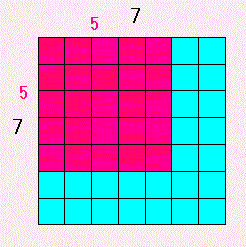
下の図で、「赤い正方形」と「青いのこり部分」とどちらが大きいか
パッと見ただけでわかりますか。
わたしの目は、あまりよくないのか
どれも「赤い正方形」の方が大きい!って思ってしまいます。
(のこりものに福があるって思えない・・・?)
|
|
|
|
|
|
じつは、こうなっています。
22 − ( 32−22 ) = −1 , つまり 「青」が 1 大きい
52 − ( 72−52 ) = 1 , つまり 「赤」が 1 大きい
122 − ( 172−122 ) = −1 , つまり 「青」が 1 大きい
この式を書きなおすと、こうなります。
22 − ( 32−22 ) = −1
−32 +22 + 22 = −1
−32 + 2×22 = 1
32 − 2×22 = 1
ほかの2つの式も、こうなります。
72 − 2×52 = −1
172 − 2×122 = 1
そうすると、
X2 − 2Y2 = 1
という式のX,Yにあてはまる整数を考えたとき
(X,Y)=(3,2) ,(7,5) , (17,12)
があてはまるってことです。
さあ、ほかにどんな数があてはまるか見つけられますか。
じつは、
X2 − aY2 = 1
のような方程式はペル方程式とよばれています。
高校になると、この方程式をみたす点(X,Y)をグラフにすると
双曲線(そうきょくせん)になるって習います。
そうすると、このことは双曲線の上の点で、
X座標もY座標も整数となるものを
さがせっていうことですね。
● 1+/2 ●
X2 − 2Y2 = 1
にあてはまる、X,Yをほかにさがそうということでしたね。
その前に、
32 − 2×22 = 1
72 − 2×52 = −1
172 − 2×122 = 1
のたねあかしをしましょう。
32 − 2×22
= ( 3+2/2 )( 3−2/2 )
= ( 1+2/2+2)( 1−2/2+2 )
= ( 1+/2 )2( 1−/2 )2
= {( 1+/2 )( 1−/2 )}2
= { 1−2 }2
= {−1}2
= 1
つまり、
( 1+/2 )2 = 3+2/2
( 1−/2 )2 = 3−2/2
にでてくる、3 と 2 が X2 − 2Y2 = 1 の解のひとつとなります。
高校生なら、2重根号のところで、
/3+2/2 =1+/2
/3−2/2 =/2−1
のようなのは見たことがありますね。
(下の方は正の数で答えないといけないので、よくまちがいますね。)
さて、まず
( 1+/2 )( 1−/2 ) = −1
です。そして、
32 − 2×22 = (−1)2
のたねあかしは、
( 1+/2 )2 = 3+2/2
( 1−/2 )2 = 3−2/2
でした。
おなじように、
72 − 2×52 = (−1)3
のたねあかしは、
( 1+/2 )3 = 7+5/2
( 1−/2 )3 = 7−5/2
です。さらに、
172 − 2×122 = (−1)4
のたねあかしは、
( 1+/2 )4 = 17+12/2
( 1−/2 )4 = 17−12/2
です。
そうすれば、あともうひとつ見つけるなら
( 1+/2 )6 = □+○/2
( 1−/2 )6 = □−○/2
を計算すればよさそうですね。
でも、だれだって6乗もしたくありませんよね〜。
(はっきり言って、6乗どころか4乗も5乗もごめんこうむりますっ!)
あと、このたねあかしのキーともいえる数 1+/2 は
基本単数(きほんたんすう)とよばれるとくべつな数ですが、
このことについては、ふかいりしないことにします。
● 連分数と数列 ●
1+/2 って、このホームページにでてきましたね。
そう、<お勉強>の「連分数」のところでは /2 が、
そして、<お勉強>の「黄金数」のところでは ずばり 1+/2 がでてきました。
こうでしたね。
1
1 + /2 = 2 + 1
2+ 1
2+ 2+
・・・
つまり、 1+/2 って、次の式をみたす X です。
1
X = 2 + X ・・・ (1)
たしかめてみると、
X2 = 2X + 1 ・・・ (2)
X2 − 2X − 1 = 0 ・・・ (3)
この2次方程式を解くと
X = 1+/2 ,1−/2
となります。
そこで、α=1+/2 ,β=1−/2 とおくことにします。
そうすると、まず
( 1+/2 )( 1−/2 ) = −1
は、 αβ=−1 ・・・ (4)
ということです。高校生なら、(3)の「解と係数の関係」として知っていますね。
さらに、(2)から
α2=2α+1 , β2=2β+1 ・・・ (5)
(1)から
1 1
α= 2+ α , β= 2+ β ・・・ (6)
さて、αで話をすすめましょう。
「黄金数」のときと同じようにしてやってみます。
α = 1+1/2
α2 = 2α+1 = 2(1+1/2)+1 = 3+2/2
α3 = 2α2+α = 2(3+2/2)+(1+1/2) = 7+5/2
α4 = 2α3+α2 = 2(7+5/2)+(3+2/2) = 17+12/2
ここで、数列
1 , 3 , 7 , 17 ,・・・
1 , 2 , 5 , 12 ,・・・
の出し方がけんとうつきますね。
最初は 1,3 で 1+2×3=7 , 3+2×7=17 ,・・・
最初は 1,2 で 1+2×2=5 , 2+2×5=12 ,・・・
「黄金数」からは、「フィボナッチ数」と「リュカ数」がでてきましたが、
今度は名前もない「 1+/2 」ですから、これまた名前もない
1 , 3 , 7 , 17 ,・・・
1 , 2 , 5 , 12 ,・・・
がでてきたというわけです。
さて、続きを考えると
7+2×17=41 , 17+2×41=99 ,・・・
5+2×12=29 , 12+2×29=70 ,・・・
そこで、じっさいにたしかめると
412 − 2×292 = (−1)5
992 − 2×702 = (−1)6
となって、
X2 − 2Y2 = 1
にあてはまる、X,Yが さらに (X,Y)=(99,70)とつけくわえられました。
ついでに、
( 1+/2 )6 = 99+70/2
( 1−/2 )6 = 99−70/2
となります。
● 1次結合 ●
「フィボナッチ数」は、「黄金数」の近似分数の分子と分母にでてきました。
さて、今回は「 1+/2 」で見てみましょう。
X1 = 1
1 1 3
X2 = 2+ --- = 2 + --- = ---
X1 1 1
1 1 7
X3 = 2+ --- = 2 + --- = ---
X2 3 3
1 3 17
X4 = 2+ --- = 2 + --- = ---
X3 7 7
とちゅうの計算を考えれば、数列
1 , 3 , 7 , 17 ,・・・
がでてくるのは、なんとなく(?)なっとくですね。では、数列
1 , 2 , 5 , 12 ,・・・
が次のようにして出てくるのはなっとくできますか。
Y1 = 1
Y2 = 2
1 1 5
Y3 = 2+ --- = 2 + --- = ---
Y2 2 2
1 2 12
Y4 = 2+ --- = 2 + --- = ---
Y3 5 5
う〜ん!なにかごまかされたみたいってとこでしょうか。
じつは、こうなるからです。
1 2α+1
α=2+--- より α=---------- となり
α α
α2 = 2α+1
ここで、問題にしている α2 が (近似分数を計算する式と同じ) αの分子 と同じということがキーです。
さあ、つづけて見てみましょう。
2α+1
次には、この α=---------- を 逆数にしていれます。
α
1 α
α=2+--- より α= 2+ ----------
α 2α+1
2(2α+1) α
α= ---------- + ----------
2α+1 2α+1
5α+2
α= ----------
2α+1
分母の 2α+1 は α2 なので、
α3 = 5α+2
やっぱり、問題にしている α3 が (近似分数を計算する式と同じ) αの分子 と同じとなりますね。
ここで、α = 1+1/2 ということを考えると、
/2 の前の数(係数)は、
2α+1=2(1+1/2 )+1
=2(1+1/2 )+1+0/2
のところだけ、つまりスタートだけ 3 にならずに 2 のままだけど、
あとは同じように近似分数の計算の分子をみればいいってことですね。
さいごに、これでやってまとめてみましょう。
| 1
2+1/1= 3/1 2+1/3=7/3 2+3/7=17/7 2+7/17=41/17 2+17/41=99/41 |
1
2 2+1/2=5/2 2+2/5=12/5 2+5/12=29/12 2+12/29=70/29 |
32 − 2×22 = 1 72 − 2×52 = −1 172 − 2×122 = 1 412 − 2×292 = −1 992 − 2×702 = 1 |
じつは、「黄金数」も基本単数です。
では、こちらではどんなふうになるのでしょうか。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001