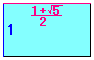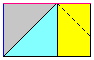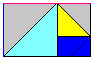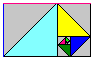フィボナッチ列(5)
● ガスケット ●
「ガスケット」っておぼえていますか。
(このホームページの「ガスケット」を見てくださいね。)
「ガスケット」というのは、
「スカスカでなかみがない」ものでしたね。
(さんすう・数学のお約束としては、これではちょっと・・・)
そして、その中でも、とりわけ有名なのがシェルピンスキー・ガスケットでした。

今回は、フィボナッチ列を使って「ガスケット」作りをしてみましょう。
● 等比数列 ●
いきなり、フィボナッチ列というのもなんですから、
まずは等比数列(とうひすうれつ)です。
等比数列(とうひすうれつ)なんて知らない〜って?
< 公比 2 >
たとえば、こんな数列です。(ちなみに、数列って数のならんだもの!)
さいしょは「1」
これを2倍すると、1×2=「2」
これをさらに2倍すると、2×2=「4」
これをさらに2倍すると、4×2=「8」
これをさらに2倍すると、8×2=「16」
・・・ってなちょうしで、どんどん2をかけていってできた数列
1 , 2 , 4 , 8 , 16 , ・・・
のようなものです。
さいしょは、「1」でなくていいし、かけるのも「2」でなくていいのです。
そんな、数列
1 , 2 , 4 , 8 , 16 , ・・・
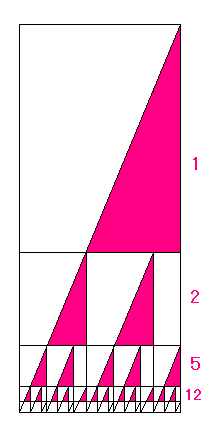
を図にしてみると・・・
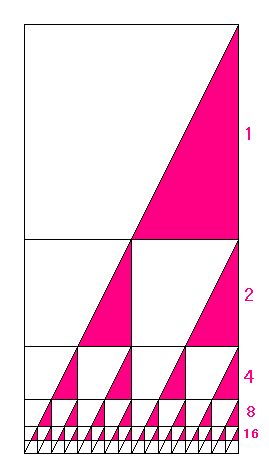
ちなみに、上の図は「黄金の長方形」ではなくって、
よこが「1」、たてが「2」
つまり対角線(たいかくせん)の傾き(かたむき)が「2」の長方形です。
この図のかきかたも、
1 , 2 , 4 , 8 , 16 , ・・・
という数列がでてくることも、相似(そうじ)ってことだけです。
そこで、・・・
|
|
|
というふうにして、シェルピンスキー・ガスケットをつくります。
えっ、こんなのシェルピンスキー・ガスケットでないって?
そんなことありません。たんに、
正三角形からはじめるか、
直角三角形からはじめるか
のちがいだけですよね。
< 公比 3 >
それでは、さいしょは、「1」のままで、
かけるのを「3」にしてみましょう。
そうすると、
1 , 3 , 9 , 27 , ・・・
という数列になります。
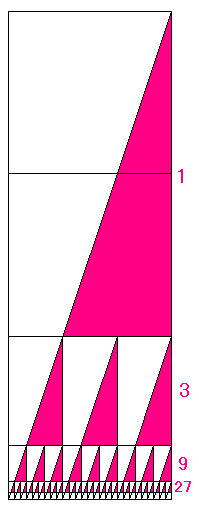
これを図にして、さらに「ガスケット」を作ると・・・
|
|
|
う〜ん!たんにシェルピンスキー・ガスケットに
もう1段(だん)つけくわえただけ・・・といったかんじですね。
ちなみに、上の図は
よこが「1」、たてが「3」
つまり対角線(たいかくせん)の傾き(かたむき)が「3」でした。
● フィボナッチ列 ●
さあ、いよいよフィボナッチ数列です。
(もう、なんどもやりましたね。)
1 , 2 , 4 , 8 , 16 , ・・・
これを図にするには、こんなことをくりかえします。
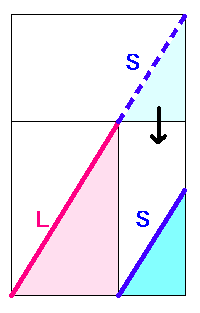
もちろん、長方形は「黄金の長方形」です。
つまり対角線(たいかくせん)の傾き(かたむき)は「黄金数」です。
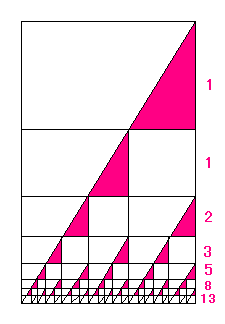
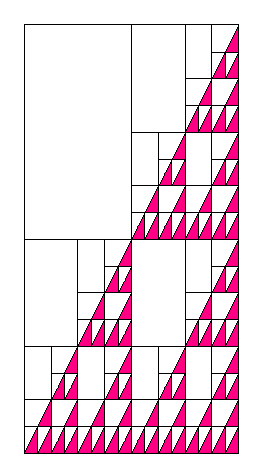
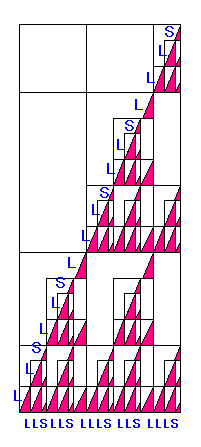
では、いよいよ「ガスケット」作りです。
作り方は、スライドさせたところに、うめこむだけです。
|
|
|
名前は、「黄金のガスケット」なんていかがでしょうか。
いえいえ、「フィボナッチ・ガスケット」の方がいいかも・・・。
(このホームページの中だけですけど・・・)
さて、こんなふうにしてできてくるフィボナッチ列は、
どんなフィボナッチ列でしょうか。
もちろん、作り方をみればすぐわかりますよね。
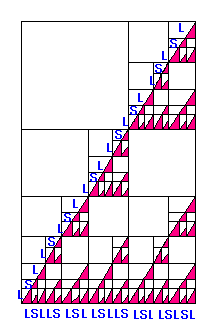
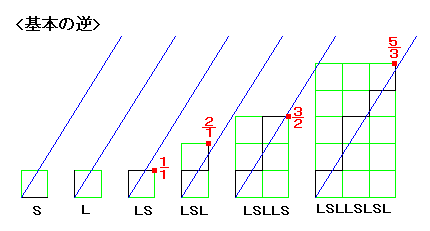
このホームページで「基本の逆のフィボナッチ列」と名づけたものです。
そう、
L -----> LS (「長い」は「長い」と「短い」に!)
としたものの方です。
S
L
LS
LSL
LSLLS
LSLLSLSL
LSLLSLSLLSLLS
LSLLSLSLLSLLSLSLLSLSL
・・・・・
これは、”次”をだすのに
”今”という土台(どだい)の上に”前”をつけたしていく、
コースがどんどんのびていくものでしたね。
● 1+/2 ●
数列
1 , 2 , 5 , 12 ,・・・
をおぼえていますか。
(このホームページの「ペル方程式」でやったのです。)
「次」の数をだすのに、「今」と「前」をたしたのがフィボナッチ数列でしたね。
1
1
1+1=2
2+1=3
3+2=5
5+3=8
それにたいして、
「次」の数をだすのに、「今」の2倍と「前」をたしたのがこの数列です。
1
2
2×2+1=5
5×2+2=12
そして、フィボナッチ数列が「黄金数」からでてきたように、
この数列は「1+/2 」からでてきました。
このホームページにも、ケータイの待ち受け画面用に作ってあります。
(<iモード>を見てくださいね。)
でも、ケータイの待ち受け画面用にしては、
「1+/2 」では幅(はば)が広すぎるので、「/2 」で作ってあります。
|
黄金数 |
/2 (1+/2 ) |
|
|
|
|
「1」づつとれる |
1+/2 なら「2」づつとれる |
数列
1 , 2 , 5 , 12 ,・・・
を図にして、さらに「ガスケット」を作ると・・・
|
|
|
こんどは、名づけて、「1+/2 のガスケット」なんていかがでしょうか。
(もちろん、このホームページの中だけですけど・・・)
さて、こんなふうにしてできてくる文字列は、
どんな文字列しょうか。
これも、作り方をみればすぐわかりますね。
そう、
S -----> L (「短い」は「長い」に!)
L -----> LLS (「長い」は「長い」が2つと「短い」に!)
とするのです。
つまり、こんな文字列です。
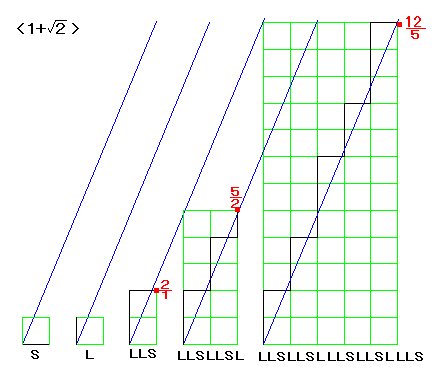
S
L
LLS
LLSLLSL
LLSLLSLLLSLLSLLLS
・・・・・
これもまた、”次”をだすのに
”今”という土台(どだい)の上に、もういちど”今”をつけたして、(つまり2倍して)
これに”前”をつけたしていく、
コースがどんどんのびていくものになっています。
でも、コースがどんどんのびていくだけなら、
”今”という土台(どだい)の上に、つけたしていけばいいだけなのです。
だったら、”次”をだすのに
”今”という土台(どだい)の上に、”前”をつけたして、
さらにもういちど”今”をつけたしても、
コースがどんどんのびていくものになります。
こんなふうにね。
S
L
LSL
LSLLLSL
LSLLLSLLSLLSLLLSL
・・・・・
これは、じつは
S -----> L (「短い」は「長い」に!)
L -----> LSL (「長い」は「長い」「短い」「長い」に!)
としたものです。
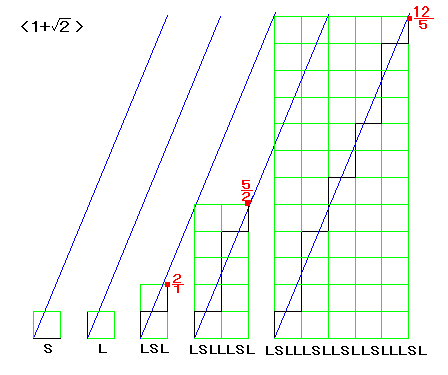
これは、L -----> LSL でわかるように、
対称的(たいしょうてき)になってきていますね。
● チェック柄 ●
せっかくですから、ついでに「チェック柄」作りもしておきましょう。
(オリジナルブランドとして売り出すのは、むりだとしても・・・)
これが、「黄金のチェック柄」でしたね。
(もちろん、このホームページだけのお話ですが・・・)

でも、いま「ガスケット」作りで出てきたのは、
このホームページで「基本の逆のフィボナッチ列」と名づけたものでした。
それを「チェック柄」にしたものは、下の図で

ちょっと回転させただけのものでした。
さて、「1+/2 のガスケット」作りの方を
「チェック柄」にしてみましょう。
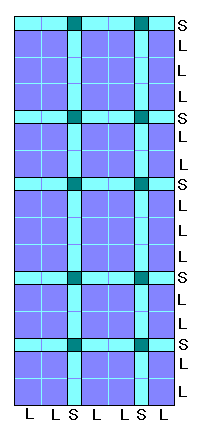
長いので、マフラーならこっちの方がいいかも・・・。
ちなみに、L -----> LSL とした方は
「チェック柄」も対称的です。
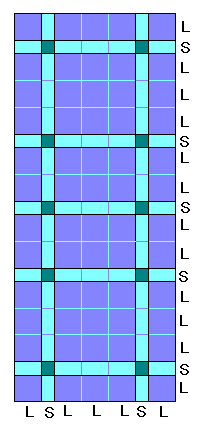
う〜ん!
でも、やっぱり微妙に(びみょうに)対称的でないものの方が、
あじがあるかも・・・(?)
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001