フィボナッチ列(6)
● 「しんぶんし」 ●
「新聞紙(しんぶんし)」って、有名(ゆうめい)ですよね。
そう!
上から読んでも「しんぶんし」
下から読んでも「しんぶんし」
子どものころに、いろいろ見つけてあそびました。
でも、このホームページのように、横書きがふつうになると
右から読んでも「しんぶんし」
左から読んでも「しんぶんし」
ってことになるかもしれませんね。
英語(?)なら、
右から読んでも「SOS」
左から読んでも「SOS」
なんてね。
・・・ということで、今回は、
右から読んでも左から読んでも同じになる、文字列のお話です。
● フィボナッチ列 ●
もちろん、まずはフィボナッチ列です。
フィボナッチ列といっても、いろいろありましたね。
たとえば、基本のフィボナッチ列は、
文字列のたし算からできたフィボナッチ列でした。
(・・・といっても、このホームページの中だけのお話でしたが。)
そこでは、さいしょに、こんなことをみてみました。
それぞれの文字列の中のSとLの比(の値)をみたのです。
S
L
SL ・・・ Sは1,Lは1で 1:1 から 1/1
LSL ・・・ Sは1,Lは2で 1:2 から 2/1
SLLSL ・・・ Sは2,Lは3で 2:3 から 3/2
LSLSLLSL ・・・ Sは3,Lは5で 3:5 から 5/3
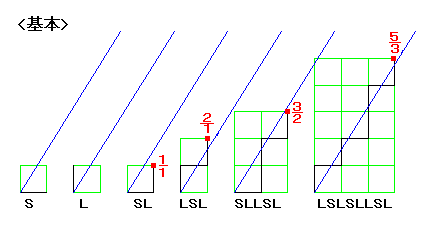
これは、基本のフィボナッチ列だけでなく、
ほかもみんなこうなっていましたね。
(ですから、これをフィボナッチ列のお約束にすればいいですね。
もっとも、今ごろになってフィボナッチ列のお約束をするのも・・・)
ところで、
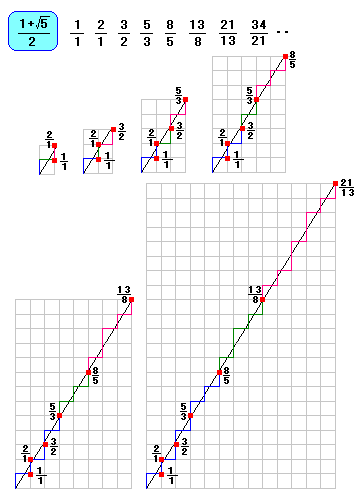
1/1 、2/1 、3/2 、5/3 、8/5 ・・・
というのは、黄金数の近似分数(きんじぶんすう)でした。
つまり、1/1 、2/1 、3/2 、5/3 、8/5 ・・・ は
黄金数にどんどん近づいていったのです。
ちなみに、つぎの近似分数を出すには、分子も分母も、
自分とその前の数をたせばよかったですね。
さて、今回はあらたに「近い」ということにこだわった、
フィボナッチ列を考えてみましょう。
えっ、何に近いのかって?
もちろん「川」にです。
傾き(かたむき)が黄金数の「青い線」を「川」にたとえるなら、
なるべく「川」に近いところを通る
ような行き方を考えようというのです。
そうしたら、それはもちろん
1/1 、2/1 、3/2 、5/3 、8/5 ・・・
を通りますから、りっぱな(?)フィボナッチ列ですね。
そんな、なるべく「川」に近いところを通るようなフィボナッチ列を、
<近似(きんじ)>のフィボナッチ列とでもよぶことにしましょう。
(・・・といっても、またまたこのホームページの中だけのお話ですが。)
● 対称 ●
まずは、<近似(きんじ)>のフィボナッチ列が
どんなものになるか見てみましょう。
(ここから、つごうにより「川」を青ではなく黒にしています。
ど〜でもいいようなことですが・・・)
< 近似 >
なるべく「川」に近いところを通るようなフィボナッチ列は・・・
こんなフィボナッチ列です。
S
L
LS
LSL
LSLSL
LSLSLLSL
LSLSLLSLLSLSL
LSLSLLSLLSLSLLSLLSLSL
LSLSLLSLLSLSLLSLLSLSLLSLSLLSLLSLSL
このフィボナッチ列を見ると、何か気づきますね。
そう、「しんぶんし」です!
|
左から読むと・・・ |
右から読むと・・・ |
|
S L LS LSL LSLSL LSLSLLSL LSLSLLSLLSLSL LSLSLLSLLSLSLLSLLSLSL |
S L SL LSL LSLSL LSLLSLSL LSLSLLSLLSLSL LSLSLLSLLSLSLLSLLSLSL
|
だんだん、あとの方になると(・・・というよりは、ずいぶん早めに)
ほぼ「しんぶんし」のようになってきますね。
これって、どうしてでしょうか。
それは、もちろん、1/1 、2/1 、3/2 、5/3 、8/5 ・・・ が
黄金数にどんどん近づいていくからです。
あとの方になると、もうほとんど「川」のまぢかですから、
スタートとゴールを入れかえて逆向き(ぎゃくむき)に進んでも、
同じようになっているはずです。
つまり、スタートからゴールに向かって進んでも、
ゴールからスタートに向かって進んでも、
同じようになっているはずです。
たとえば、スタートから、
「上右上右上上右上」と「川」に近い所を通るなら、
じゅうぶんあとの方のゴールからなら、
「下左下左下下左下」と「川」に近い所を通るってことです。
もっとも、どこをゴールにするかは大問題です。
だって、スタートとゴールから、まるで鏡を見ているように
「上」なら「下」、「右」なら「左」
といったぐあいに同時に進めてみると、まん中あたりで、のこり、
たて方向に1つで、横方向にも1つ
となってくると、(それは、分子も分母も奇数のときですね)
スタートからは「上」なのに、ゴールからは「左」とか、
スタートからは「右」なのに、ゴールからは「下」とか、
ならざるをえなくなりますからね。
ここまでをまとめると、「近道は対称(たいしょう)を好む」
なんちゃって・・・ね。
(「自然は対称を好む」をもじっただけです。
ちなみに、「近道」というのは、「川」に近いということで、
道のりが短いということではありません。あしからず!)
● 中間近似分数(1) ●
もっといろいろ「近道」をみてみましょう。
(くりかえしますが、「近道」というのは、「川」に近いということで、
道のりが短いということではありません。)
えっ、「近道」なんて一通りだって?
そうじゃなくって、ちがう「川」で考えようというのです。
なにも「川」(の傾き)は、「黄金数」である必要(ひつよう)はありませんからね。
< /2ー1 >
黄金数は、連分数であらわすと、 ず〜っと 1 が続く数でした。
それなら、連分数であらわすと、 ず〜っと 2 が続く数は?
それは、前回もやりましたね。
1
1 + /2 = 2 + 1
2+ 1
2+ 2+
・・・
です。
でも、パソコンの画面が横長ということもあって、
さいしょの 2 だけとった数の /2−1 を考えてみましょう。
さて、この数の近似分数は、とちゅうまで計算すると、
1/2 , 2/5 , 5/12 , 12/29 ・・・
となります。
ちなみに、つぎの近似分数を出すには、分子も分母も、
自分を2倍した数と、その前の数をたせばいいですね。
そうすると、
分子が偶数なら分母は奇数、分子が奇数なら分母は偶数となって、
分子も分母も奇数になることはありません。
だったら、どこをゴールにするかを気にしなくても、
そのうち、「しんぶんし」になりそうですね。
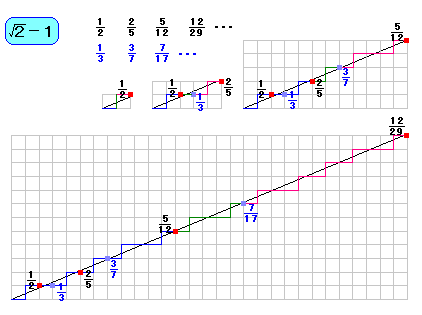
さて、なるべく「川」に近いところを通るような文字列は・・・
こんな文字列になってきますね。
S
L
SL ・・・ Sは1,Lは1で 1:1 から 1/1
SLS ・・・ Sは2,Lは1で 2:1 から 1/2
SLSSSLS ・・・ Sは5,Lは2で 5:2 から 2/5
SLSSSLSSLSSLSSSLS ・・・ Sは12,Lは5で 12:5 から 5/12
これって、名もない文字列です。
さすがに、このホームページでも、いちいち名前をつけたりはしません。
さて、同じように考えて、
さっそく、スタートとゴールから同時に進んでみましょう。
S
L
SL
SLS
SLSSSLS
SLSSSLSSLSSLSSSLS
SLSSSLSSLSSLSSSLSSLSSSLSSLSSSLSSLSSLSSSLS
だんだん、あとの方になると(・・・というよりは、またしてもずいぶん早めに)
「しんぶんし」になっていますね。
さて、ここで、この数の近似分数の
1/2 , 2/5 , 5/12 , 12/29 ・・・
のほかに、どんなところを通るかを見ていくことにしましょう。
まずは、「SLSSSLS」で見てみましょう。
もうすでに、「しんぶんし」になっているとすると、
スタートから「SLS」と行けば、ゴールからも「SLS」とくることになります。
ということは、「SLSSSLS」の2/5から、「SLS」の1/2もどった
2−1 1
-------- = ----
5−2 3
のところを通ることになります。
同じように、もうすでに「しんぶんし」になっていたとしたら・・・
5−2 3
-------- = ----
12−5 7
12−5 7
-------- = ----
29−12 17
というところを通ることになります。
さて、こうしてでてきた
1/3 , 3/7 , 7/17 , ・・・
はどんな数でしょうか。
それは、もとの近似分数
1/2 , 2/5 , 5/12 , 12/29 ・・・
の(それぞれの間の)中間近似分数とよばれているものです。
1/2 , 2/5 , 5/12 , 12/29 ・・・
1/3 , 3/7 , 7/17 , ・・・
● 中間近似分数(2) ●
もちろん、中間近似分数というのは、
間にたった1つだけあるというわけではありません。
そのことを、連分数であらわすと、 ず〜っと 3 が続く数から、
(パソコンの画面が横長ということで、)さいしょの 3 だけとった数の
(/13−3)/2 でみてみましょう。
1
(/13 −3)/2= 1
3+ 1
3+ 3+
・・・
さて、この数の近似分数は、とちゅうまで計算すると、
1/3 , 3/10 , 10/33 , ・・・
となります。
ちなみに、つぎの近似分数を出すには、分子も分母も、
自分を3倍した数と、その前の数をたせばいいですね。
そうすると、こんどは分子も分母も奇数になることがあって、
どこをゴールにするかが問題になってきます。
でもまあ、そのうち、ほぼ「しんぶんし」になるってことでいいですね。
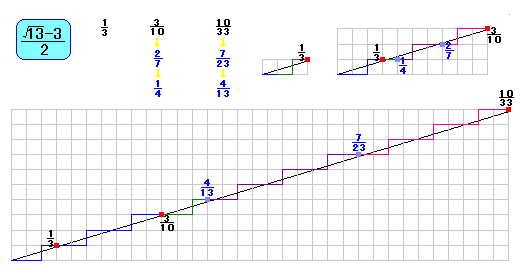
さて、1/3 と 3/10 の間の中間近似分数をみてみましょう。
3−1 2
-------- = ----
10−3 7
とまず1つ見つかりますね。でも、さらに
2−1 1
-------- = ----
7−3 4
と見つかります。
ついでに、3/10 と 10/33 の間の中間近似分数もみてみましょう。
10− 3 7
-------- = ----
33−10 23
7− 3 4
-------- = ----
23−10 13
● 中間近似分数(3) ●
ゴールからバックして中間近似分数を見つけたので、
なぜか、コースまでバックしてくりかえされそうに、
かんちがいしそうですね。
でも、そんなはずはありません。
そう、スタートとゴールから、まるで鏡を見ているように
「上」なら「下」、「右」なら「左」
といったぐあいに同時に進むはずです。
けっして、コースまで、
ゴールからバックして、くりかえされるのではありません。
中間近似分数のところは、あくまでもそこを通るというだけです。
このことを、連分数であらわすと、 ず〜っと 4 が続く数から、
(パソコンの画面が横長ということで、)
さいしょの 4 だけとった数の
/5−2 で見てみましょう。
1
/5 −2 = 1
4+ 1
4+ 4+
・・・
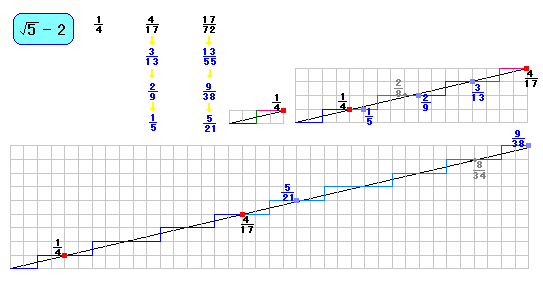
ほらね。
たとえば、右上の図の 4/17 をゴールとするコースでは、
4/17 から 3/13 までバックするのと
3/13 から 2/9 までバックするのとでは、
同じくりかえしですが、
2/9 から 1/5 までバックするのとでは、
ちがっていますね。
でも、たしかに 1/5 は通っています。
そして、1/5 を通りながら、
「しんぶんし」になるように進んでいますね。
じつは 17/72 をゴールとするコースもかきたかったのですが、
パソコンの画面に入りきらなかったので
中間近似分数の 9/38 までの図としてしまいました。あしからず!
● 中間近似分数(3) ●
ここまで、ず〜っと 1 やら 2 やら 3 やら 4 が
つづく数ばかりやってきたので、さいごに、
1,2,1,2・・・ とたがいちがいにつづく数でしめくくる(?)ことにしましょう。
1
/3 −1 = 1 + 1
2+ 1
1+ 1
2+
・・・
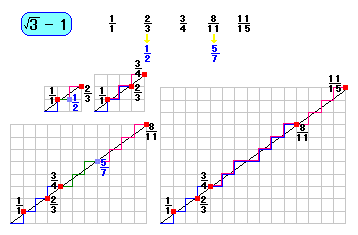
この図を見ると、
スタートとゴールから、まるで鏡を見ているように
「上」なら「下」、「右」なら「左」
といったぐあいに同時に進むのはいいですが、
重なるばあいもでてきて、ややこしいですね。
さて、今回の
なるべく「川」に近いところを通るような行き方はどうでしたか。
えっ、もう「川」には近づきたくないって?
そうそう、「よい子は、川に近づかない」でしたね。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001