ペンローズ・タイル
● ペンタグラム ●
ペンタグラムといったら・・・
そう、あのピタゴラス教団のシンボルマークです。
もう、このホームページでは、おなじみですね。

だったら、ペンローズなんだから・・・

きっと、ペンタグラムのローズ(バラの花)だろうって?
ざんねんでした。
ペンローズというのは、人の名前なのです。
その人は、2種類(しゅるい)のタイルを発明(?)して、
無限(むげん)に広がる平面を「タイルばり」してみせたのです。
えっ、無限(むげん)に広がる平面なんて、
一生かかっても「タイルばり」できっこないって?
もちろん、その方法を考えただけです。
そのタイルばりが、
ちょっとそれまでになかったようなものなので、(非周期的といわれるもの)
とっても有名になりました。
● 相似 ●
さあ、どんなタイルなのでしょうか。
わくわく、どきどきですよね。
きっと、見たこともないタイルだよね〜って?
これまた、ざんねんでした。
じつは、中学生ならきっと一度は見たことがあるものなのです。
図形の相似(そうじ)のお勉強のところでです。
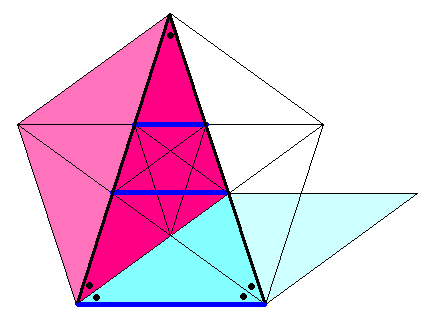
まん中の三角形を見たことありますよね。
角の大きさが 1:2:2 の比になっている三角形です。
この三角形を、図のように「赤」と「青」に切ると、
「青」の三角形は、切る前のもとの三角形と相似(そうじ)でした。
ペンローズ・タイルというのは、
この「赤」と「青」の三角形を図のようにくっつけて、
ひし形にしたものです。
そして、この2種類(しゅるい)のタイルをつかって、
平面をすき間なくうめていったのです。
つまり、ジグソーパズルのようなものです。
たとえば、こんなふうになります。

もちろん、あとはこの「かたまり」を使って、
どんどん平面をうめていこう・・・なんていうのはダメですよ。
そういうのは、周期的(しゅうきてき)といって、
めずらしくもなんともないのです。
ちなみに、こんなソロバンの玉のような形にしたのは、
なんのふかい意味もありません。
2種類のタイルのどちらかから始めてもよかったのですが、
それだと、ステップが多くなって、めんどうだっただけです。
● 拡大・縮小 ●
このペンローズ・タイルを使って、
いきなり「タイルばり」をはじめたら・・・
さあ、たいへん!
無限(むげん)に広がる平面どころか、
あっという間に、行きづまってしまいます。
では、どうするかって?
なにごとも、計画(けいかく)が大切ですね。
今回は、計画を図にしてしまうのです。
さしづめ、「タイルばり」の設計図(せっけいず)です。
では、これから、その設計図(せっけいず)を書いていきましょう。
たとえば、下の図からはじめます。
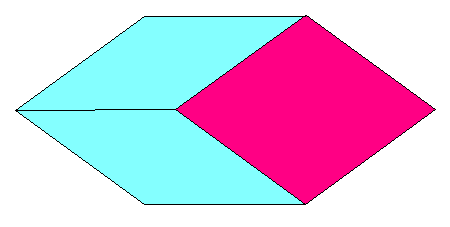
これを、どんどんこまかくしていくのです。
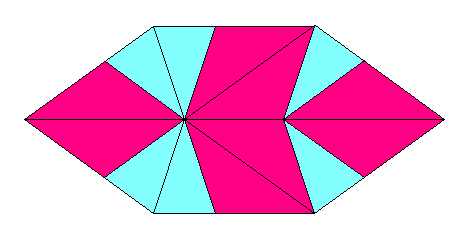
どんどん、どんどん・・・。
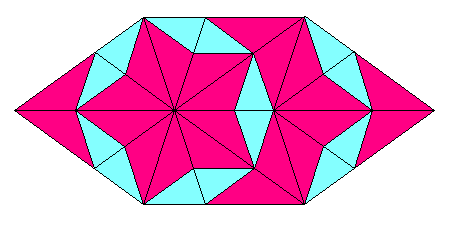
もっと、どんどん、どんどん・・・。
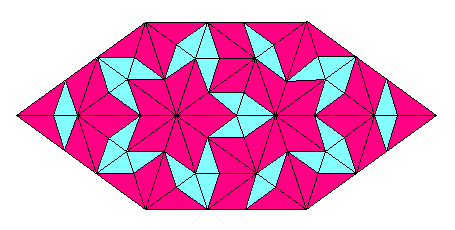
もっともっと、どんどん、どんどん・・・。

もっともっともっと、どんどん、どんどん・・・。

もちろん、もっともっともっともっと・・・こまかくしていけます。
いつまでも、いつまでも・・・
そう!無限(むげん)にこまかくしていけるのです。
・・・ということは?
これを拡大(かくだい)した設計図(せっけいず)を見ながら、
どんな大きな壁(かべ)だって、みごとに「タイルばり」ができるってものです。
もちろん、どこか気に入った部分(ぶぶん)をとりだして、
そこから、どんどん細かくしていってもいいですね。
● 黄金比 ●
では、どういうルールで、こまかくしていったのでしょうか。
もちろん、こまかくするといっても、
もとのタイルと形は同じです。
つまり、相似(そうじ)です。
この相似比には、あの黄金比が登場します。
くわしくは、このホームページの
「ペンタグラム」、「黄金数」、「フィボナッチ数」、「母関数」などを見てくださいね。
ちなみに、下の図は「母関数」にのせてあります。
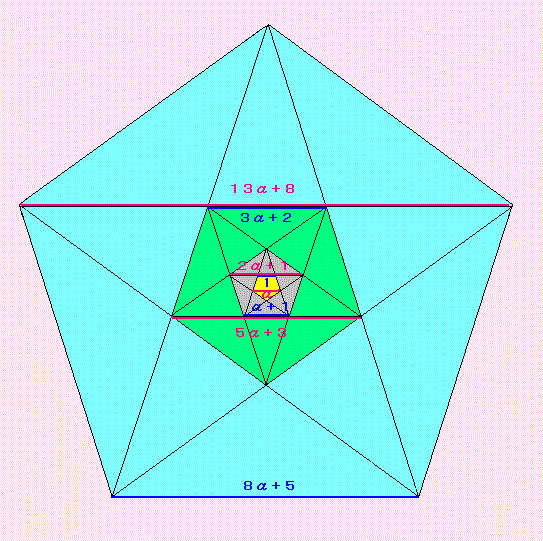
でも今回は、相似比については、立ち入らないでおきましょう。
さて、こまかくするといっても
ちぢめて小さくするだけなら、かんたんですが、
それでジグソーパズルのように、くみあわせるとなると・・・。
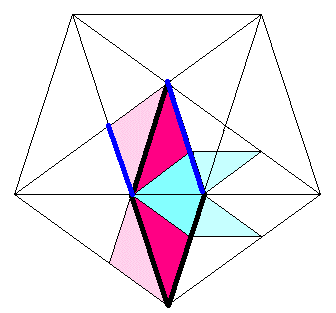
じつは、もうすでに、2種類のうちの細(ほそ)い方のタイルは、
すでに、こまかくする方法をお知らせしてあるのです。

まん中の三角形を2つ、(たてに)くっつけると、
ペンローズ・タイルの細い方(の1まわり大きいもの)です。
そして、そのこまかくする方法は、
もうやりましたよね。
この三角形を、図のように「赤」と「青」に切ると・・・、
そう、「青」の三角形は、切る前のもとの三角形と相似(そうじ)でした。
ですから、それを2つくっつけたものは、
もとのペンローズ・タイルの細い方と相似です。
さらに、のこった「赤」の三角形を2つくっつけると、
今度はペンローズ・タイルの太い方と相似です。
これを、(2まわり)小さいサイズで図にすると・・・
さて、では太い方のタイルは、
どのように、こまかくするのでしょうか。
それが、下の図です。
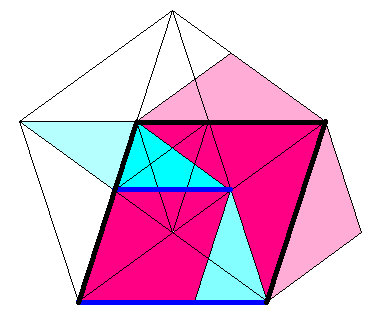
なんといっても、相似比に黄金数が出てくるだけあって、
ペンタグラムが大活躍(だいかつやく)ですね。
そして、ペンローズは、このジグソーパズルのようなかみあわせが、
うまくいくってことを見つけたのです。
しかし、どんな教科書にものっているほど、
平凡(へいぼん)きわまりない三角形から、こんなことを考えつくなんて・・・。
やっぱり、ただものではありませんね。
● 線対称 ●
さっき、どこか気に入った部分(ぶぶん)をとりだして、
そこから、どんどん細かくしていってもいいってことでしたよね。
そこで、さっそく正10角形の部分をとりだして、
どんどんこまかくしていきました。
それが、下の図です。
5角形に広がっていて、とってもきれいですね。

ところで、ペンローズは、さいしょから
ひし形のタイルを考えたのではありませんでした。
じつは、さいしょは、こんな2種類のタイルをつかったのです。
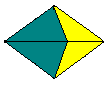
これをつかうと、たとえば、さっきの正10角形は、
こんなふうになります。

そして、じ〜っとみつめると・・・
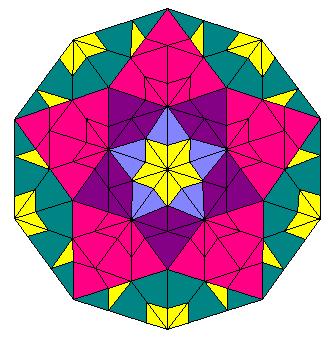
や〜っぱり、ペンタグラムのローズ(バラの花)です。
「名は体を表す」というけれど・・・もしかして?
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001