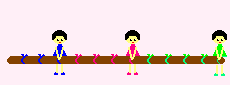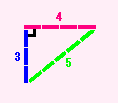ピタゴラス数

●　縄張り師　　●

　　校庭のど真ん中に、大きな直角をかいてみようって言われたらどうしますか。

　まさか、先生用の大きな三角定規（さんかくじょうぎ）をもちだして
それをのばして書こうなんて・・・。
　そんなことしたら、のばせばのばすほど、ずれてきてしまいますね。

　こんなふうにするといいのです。

　１本の「なわ（ロープ）」を用意します。
　そして、同じ長さになるように、折りたたんでは目印（めじるし）をつけていきます。

　それから、３：４：５　のところで折り曲げます。
　そうすると、一番長い辺（斜辺）の「５」に向かい合った角が直角になるのです。

　このことは、ずっと昔から（なんと紀元前から）知られていたそうです。

　すごいですね〜。

　でも、よく考えてみたら、直角もつくれないようでは
ピラミッドが建てられるはずないですよね。

●　ピタゴラスの定理　　●

　（３，４，５）　のように、直角三角形の３辺になる整数（の組）を、
ピタゴラス数といいます。

　（３，４，５）の他にどんなものがあるか知っていますか。
　なんと、そんな数は無限に多くあるのですよ。

　さあ、これからピタゴラス数を見つけていきましょう。
（高校生以上の人なら、お勉強したことあるって人も多いはずです。）

　さて、ピタゴラスの定理（三平方の定理）というのは知っていますね。

　直角三角形の３辺を　ａ，ｂ，ｃ　とすると

　　　　　ａ^２　＋　ｂ^２　＝　ｃ^２　　　・・・ (1)

となるし、その反対（逆）に三角形の３辺の間に（１）の関係がなりたてば
その三角形は直角三角形だよ、というものです。

　ａ＝３，ｂ＝４，ｃ＝５　とすると

　　　　　ａ^２　＋　ｂ^２　＝　９　＋　１６
                          　＝２５

　　　　　　　　　　ｃ^２　＝２５

ですから、たしかに（１）がなりたちますね。

　そこで、（１）をみたす（正の）整数　ａ，ｂ，ｃ　を
（３，４，５）のほかにどんなのがあるかさがしていきましょう。

　いろいろなやり方があるのですが、今回はグラフを使いますね。

　まず、(1)の両辺を　ｃ^２　でわると

　　　　ａ^２　　　　ｂ^２
　　　　ｃ^２　＋　ｃ^{２　　＝　１　　　・・・　（２）}

　そこで、（１）のかわりに

　　　　　Ｘ^２　＋　Ｙ^２　＝　１　　　・・・ (３)

　ここで、Ｘ，Ｙ　が（正の）分数（有理数といいます）であるものをさがすことにします。

　下の図でいうと、（４，３，５）のかわりに（４/５，３/５）をみつけようということです。

　ついでに、（３，４，５）の三角形も（４，３，５）の三角形も合同ですから
ａの方がｂより長いか等しいということにしておきましょう。
　といっても、ａとｂが同じ長さのときはｃは整数どころか分数にもならないので
やっぱり、ａの方がｂより長いということにしておきます。

　そうすると、

　　　　　　　　　　Ｘ　＞　Ｙ　　・・・　（４）

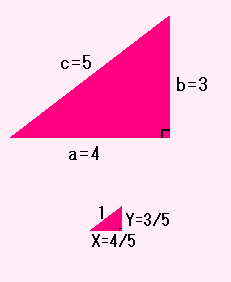
●　円と三角関数　　●

　さて、いよいよ

　　　　　Ｘ^２　＋　Ｙ^２　＝　１　　　・・・ (３)

　ここで、Ｘ，Ｙ　が（正の）分数（有理数といいます）で

　　　　　　　　　　Ｘ　＞　Ｙ　　・・・　（４）

となるものをさがしていきます。

 　（ここのお話を中学生向きに図形でやる方法は、
＜Q＆A＞の「図形でピタゴラス数」にのせてありますので、ぜひ見てくださいね。
　ここでは高校生向きにしてあります。）

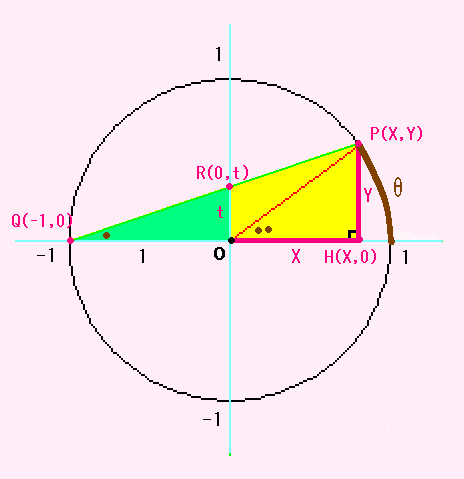
　（３）をみたす点（Ｘ，Ｙ）の集まりは、
（４）は無視して正の数も負の数も分数以外の数（無理数）も全部いれると、
中心が原点（０，０）で半径１の円ですね。

　ちなみに、弧ＳＰの長さをθとすると

　　　Ｘ＝ｃｏｓθ　　，　Y＝ｓｉｎθ　・・・　（５）

ですから、この　ｓｉｎθ　や　ｃｏｓθ　が分数（有理数）になるものを
みつけようということです。

　そこで、直線ＰＱの傾きを　ｔ　とします。

　　　　　　Ｙ　　　
　　　　１　＋　Ｘ　　^{＝　ｔ　　・・・　（６）}

　ちなみに、このことは

　　　　　　ｓｉｎθ　　　
　　　　１　＋　ｃｏｓθ　^{＝　ｔａｎ （θ/２）　　　　　・・・　（７）}

ということに対応しています。

　さて、ＸやＹが分数ならば、（６）から ｔ も分数ですね。

　　　ＸやＹが分数　−−＞　ｔ　が分数

　じつは、この逆もいえるというのです。

　　　ｔ　が分数　−−＞　ＸやＹが分数

　これから、このことをみていきましょう。

　ところで、（４）の　Ｘ　＞　Ｙ　ということは、

　　　　　ｔ　＜　ｔａｎ（π/８）＝/２　−１

ということです。

　さて、０＜ｔ＜/２　−１　をみたす分数ｔを１つ選んで点Ｒをとります。
　そして、点Ｑと点Ｒと結んで直線ＱＲと円との交点をＰ（Ｘ，Ｙ）とします。

　直線ＱＲの式は、傾きも、ｙ切片も　ｔ　ですから

　　　　　ｙ　＝　ｔ ｘ ＋ ｔ

　　　　　ｙ　＝　ｔ（ｘ＋１）　・・・　（８）

となります。P（X，Y）がこの直線上にあるということは式（６）と同じです。

　さあ、ｔ　が分数なら、はたして　Ｘ，Ｙ　が分数になるのでしょうか。

　点Ｐは円と直線の交点ですから、連立方程式（３）（８）の解です。

　　　　　ｘ^２　＋　ｙ^２　＝　１　　　・・・ (３)

　　　　　ｙ　＝　ｔ（ｘ＋１）　・・・　（８）

　解いてみましょう。

　（８）を（３）に代入すると

　　　　　ｘ^２　＋　｛ｔ（ｘ＋１）｝^２　＝　１

　　　　　ｘ^２　＋　ｔ^２（ｘ^２＋２ｘ＋１）　＝　１

　　　　　（１＋ｔ^２）ｘ^２　＋　２ｔ^２ｘ　＋　ｔ^２−１　＝　０　　・・・　（９）

　さて、円と直線ＱＲの交点はＰ（Ｘ，Ｙ）とＱ（−１，０）ですから
（９）の解をｘ＝α　，βとすると、それは　ｘ＝Ｘ，−１です。

　ここで、高校生とくに受験生のみなさんにおなじみの
「解と係数の関係」を用いると

　　　　　　　　　　　　　　　　　２ｔ^{２
　　　　α　＋　β　＝　−}　１＋ｔ^２

　これから

　　　　　　　　　　　　　　　　　２ｔ^{２
　　　　Ｘ＋（−１）＝　−}　１＋ｔ^２

　　　　　　　　　　　　　　　　２ｔ^{２
　　　　　　　　Ｘ　＝　−}　１＋ｔ^{２　　　　＋１}

　　　　　　　　　　　　　　１−ｔ^{２
　　　　　　　　Ｘ　＝}　１＋ｔ^{２　　　　・・・（１０）}

　ｙ座標のＹは（８）から

　　　　　　　　Ｙ　＝　ｔ（Ｘ　＋　１）

　　　　　　　　　　　　　　　１−ｔ^{２
　　　　　　　　Ｙ　＝　ｔ（}　１＋ｔ^{２　　＋　１　）}

　　　　　　　　　　　　　　　２ｔ　　
　　　　　　　　^Ｙ　＝　１＋ｔ^{２　　　　・・・（１１）}

　これで、ｔが分数なら、（１０）（１１）からＸとＹも分数とわかりました。

　ちなみに、（１０）（１１）は

　　　　　　　　　　　　　　　　　１−ｔａｎ^２（θ/２）　
　　　　　　　^{ｃｏｓθ　＝}　１＋ｔａｎ^２（θ/２）^{・・・（１２）}

　　　　　　　　　　　　　　　　　２ｔａｎ（θ/２）　　
　　　　　　　　^{ｓｉｎθ　＝}　１＋ｔａｎ^２（θ/２）^{・・・（１３）}

に対応しています。

●　ピタゴラス数　　●

　０＜ｔ＜/２　−１　をみたす分数ｔは無限に多くありますから、
ピタゴラス数も　（３，４，５）だけでなくって無限に多くあることになります。

　では、いくつか計算してみましょう。

＜ｔ＝１/３＞

　ｔ＝１/３　を（１１）（１２）に入れて計算します。

　これから　（３，４，５）の直角三角形がでます。

＜ｔ＝１/５＞

　ｔ＝１/５　を（１１）（１２）に入れて計算します。

　これから　（５，１２，１３）の直角三角形がでます。

＜ｔ＝１/４＞

　ｔ＝１/４　を（１１）（１２）に入れて計算します。

　これから　（８，１５，１７）の直角三角形がでます。

●　円と２次方程式　　●

　さて、どうしてこんなにうまく話がすすんだのでしょうか。

　そのわけの１つは、２次方程式にありそうです。

　円と直線の交点をもとめるとき、２次方程式（９）がでてきました。
　（３次方程式がでてくるはずありませんよね。）

　２次方程式って、解が２個しかありませんから、
「解と係数の関係」から、（２次方程式の係数が全部分数のとき）
片方の解が分数なら、もう片方の解も分数ってすぐにわかってしまうのです。

　そして、その片方の分数の解を　ｘ＝−１　つまり点Q（−１，０）のｘ座標と
あらかじめきめておいたので・・・。

HOME（もどる）

掲載内容の無断転載、転用、編集を禁じます。(c) 小林吹代
All Rights Reserved, （c）kobayashi fukiyo , 2001