連分数
● A3,A4,B3,B4 ●
「ちかごろ、Aサイズでないとだめなんだ。
わら半紙では、Bサイズだし・・・。」
もちろん、洋服のサイズのお話ではありません。
「紙」のサイズ(規格)を話題にしているんです。
でも、これからのお話には、
AサイズだろうがBサイズだろうがどちらでもいいんです。
とりあえず、紙を1枚用意してください。
でも、正方形の「おり紙(色紙)」ではだめですよ。
A3,A4,B3,B4,・・・ といったサイズの紙です。
そんなのな〜い、って?
わら半紙がなくったって・・・、ノートを1枚やぶらなくったって・・・、
いつも新聞に入ってくる「折り込みちらし」というものがあります!
あれって、だいたいA3,A4,B3,B4,・・・ といったサイズなんですよ。
用意できましたか?
では、おり紙をしましょう。

まず、点Aが直線BC上にくるようにおりまげます。
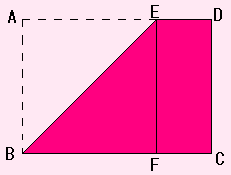
つぎに、直線BE と 直線BF がかさなるようにおります。
つまり、角EBFを二等分するようにおります。
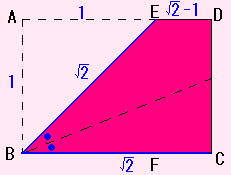
そうすると、点E と 点C がぴったりかさなるでしょ!!
ということは・・・・・。
そう、もともとの紙(長方形)は たてとよこの比が、
正方形の対角線の長さになるようになっていたのです。
AB : BC = 1 : /2
● 相似 ●
どうして、たてと横の比が 1:/2 になるようにしてあるのでしょうか。
そのことをみるために、今度は同じ大きさの紙を2枚用意しましょう。
えっ、今日の「ちらし」は全部大きさがちがっているって・・・。
それなら、1枚の「ちらし」をきっちり半分に切ってください。
(長い方の辺を半分にしてね。)
とにかく、さっき使ったくしゃくしゃになった紙ではなく、
おり目のついていない新しいのを用意してください。
そうしたら、一方はそのままにして、もう片方は図のように半分に切ります。
そして、それぞれの長方形の対角線に(1本だけ)おり目をつけます。
 |
と、その半分 |
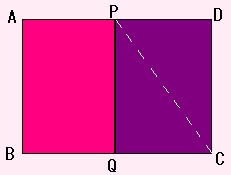 |
それを、(てきとうに回転させたり、うらがえしたりして)重ねると、
下の図のように、対角線がかさなります。
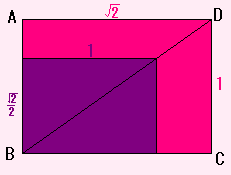
これって、半分に切ってできた長方形ともとの長方形が相似ってことです。
じっさい、
/2
2 : 1 = /2 : 2
= /2 : (/2)2
= 1 : /2
ということは・・・、
紙のサイズは、どんどんどんどん半分にきっていっても、
もとの紙と相似になるようにくふうしてあるのですね。
● 連分数 ●
さて、せっかくですから、ここで
ユークリッドの互除法(の無理数版?)をやってみましょう。
ユークリッドの互除法を知らな〜い、っていう人は
<お勉強>の「ユークリッドの互除法」を見てね。
ここでは、どんどん正方形でうめていくってことを、まねしてみます。
はやい話が、どんどん(できるだけ大きい)正方形を切り取っていくのです。
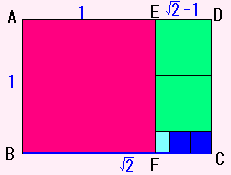
< /2 と 1 >
まず、もとの長方形は /2 と 1です。
まず
/2 ÷ 1 = 1 あまり (/2−1)
とします。(こんなわり算の書き方は、学校ではしないでね。)
これは、/2 から1が1つとれて、(/2−1)のこったということです。
< 1 と (/2ー1) >
次に、今度は反対に 1 から (/2−1)がいくつとれるか見てみます。
1
1 ÷ (/2−1) = /2−1
/2+1
=(/2−1)(/2+1)
/2+1
= 2 − 1
= /2+1 ・・・・・ (1)
= 2 +(/2−1) ・・・ (2)
ですから、商は 2 ですが、
あまりは 1 から (/2−1)の2倍の長さをひいたものです。
1−2(/2−1) = 3−2/2
ですから、
1 ÷(/2−1) = 2 あまり (3−2/2)
< (/2−1) と (3−2/2) >
さらに今度は、(/2−1) から (3−2/2) がいくつとれるか見てみます。
(/2−1)
(/2−1) ÷ (3−2/2) = (3−2/2)
(/2−1)(3+2/2)
= (3−2/2)(3+2/2)
3/2+4−3−2/2
= 9 − 8
= /2+1 ・・・・・ (3)
= 2 +(/2−1)
となり、やっぱり 商は 2ですが、
あまりは (/2−1) から (3−2/2)の2倍の長さをひいたものです。
(/2−1) − 2(3−2/2) = 5/2−7
ですから、
(/2−1) ÷(3−2/2) = 2 あまり (5/2−7)
< 相似 >
続けてやる前に、(1)と(3)がいっしょであることに気づきますね。
これは、下の2つの長方形が相似だってことです。
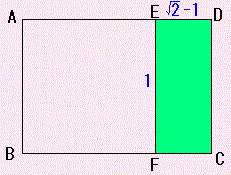 |
と |
 |
そうすると、どんどん小さくなって同じことがくりかえされるだけです。
つまり、正方形は2個とれて、「はんぱ」がでてくることのくりかえしです。
< 連分数 >
このことを、分数であらわしてみます。
/2 = 1 + (/2−1)
1
= 1 + 1 ・・・ (4)
/2−1
1
= 1 + 2+(/2−1)
ここのところは (2)の
1 ÷ (/2−1) = 2 +(/2−1) ・・・ (2)
です。
そして、
1
= 1 + 1
2+ 1
(/2−1)
ここから (長方形が相似となって
(/2−1)
(/2−1) ÷ (3−2/2) = (3−2/2)
が
1
/2−1
と等しくなって、)あとは同じくりかえしとなって
1
/2 = 1 + 1
2+ 1
2+ 2+
・・・
となります。
ちなみに、(4)のように
1
(/2−1) = 1
/2−1
というように、分子と分母を入れかえることは
互除法では、たがいちがいに(お互いに)わり算をするってことです。
/2 = 1.41421356・・・ (一夜一夜に、ひと見頃・・・)
が/2の小数でのあらわし方なら、これは/2の分数でのあらわし方です。
こんな分数は、連分数(れんぶんすう)とよばれています。
分数の方が、ず〜っと 2 が続いていてとってもきれいですね。
ところが、ず〜っと続くのが気に入らなかった人がいるのです。
なんと、ピタゴラスの定理を発見したピタゴラス(教団)自身です。
ピタゴラスの定理によると、正方形の対角線は2乗して2になる数、つまり/2 です。
ところが、いままで見てきたように、正方形の一辺と対角線の比は
いつまでたっても「はんぱ」がでてくる・・・。
これって、ふつうなら、
こ〜んなにおもしろいこと見つけた〜!大発見!!っていうことで、
みんなにじまんしそうなものなのに、
自分たちの主義・信条にあわない・・・ということで、
ひたかくしにかくしたとのことです。
● 22/7 ●
22/7 (7分の22)って有名ですね。
そう、円周率πの近似値(きんじち)です。
円周率πの近似値として、ふつうは小数の 3.14 を使います。
でも、分数では 22/7 を使うことが多いようです。
ついでですから、3.14 に近い分数を
ユークリッドの互除法を使って求めてみましょう。
まず、約分しておきます。
314 157
100 = 50
ここから、 157 と 50 でユークリッドの互除法を使います。
157 7
157 ÷ 50 = 3 あまり 7 , これは 50 = 3 + 50
50
1
50 ÷ 7 = 7 あまり 1 , これは
7 = 7
+ 7
これを、分数にあらわしてみます。
314 157
100 = 50
7
= 3 + 50
1
= 3 + 50
7
1
= 3 +
1
7+
7
1
ここで、 7
を切り捨てると
1
3.14 = 3 + 7
22
= 7
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001