素数と素因数分解

●　素数　●

　素数（そすう）ってどんな数か知っていますか。

　整数のお話です。
　ボールの箱づめで考えましょう。
　１列（行）にしかならべられなかったら素数、
何列（何行）かにならべられたら素数ではありません。

　ですから、素数かどうかということは、
１０進法とか２進法とかの数のあらわし方には関係しません。

　たとえ、こたつの上でひまそ〜にしている
「ねこの手」（何本指かな？）をかりたって、
箱にならべられるかどうかには関係しそうにもありませんからね。

　さあ、じゅんにみてみましょう。

■　１　は素数ではありません。（ちょっと特別な数なのです。）

　　　　　　●

■　２　は素数です。（偶数では、たったひとつの素数です。）

　　　　　　●●　も　●　も１列です。
　　　　　　　　　　　　●

■　３　は素数です。

　　　　　　●●●　も　●　も１列です。
　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　 ●

■　４　は素数ではありません。

　　　　　　●●　　と２列にならべられます。
　　　　　　●●
　　　　　　２×２

　　　　４＝２×２　と　４　は　２を２つかけ算してつくることができます。
　　　　２は数をつくる原料のようなもので、数の素（もと）ということから素数、
　　　　４はそれらから合成してできるので合成数という名前がついています。
　　　　合成のしかたは、かけ算です。

■　５　は素数です。

　　　　　　●●●●●　も　●　も１列です。
　　　　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　　　　 ●

■　６　は素数ではありません。

　　　　　　●●●　　や　　●●　のようにならべられます。
　　　　　　●●●　　　　　 ●●
　　　　　　　２×３　　　　　 ●●
　　　　　　　　　　　　　　　　３×２

　　　　　　６＝２×３　も　６＝３×２　もかける順番をのぞけば同じです。

■　７　は素数です。

　　　　　　●●●●●●●　も　●　も１列です。
　　　　　　　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　　　　　　　 ●
　　　　　　　　　　　　　　　　　　　 ●

■　８　は素数ではありません。

　　　　　　●●●●　　や　　●●　のようにならべられます。
　　　　　　●●●●　　　　　 ●●
　　　　　　　２×４　　　　　　  ●●
　　　　　　　　　　　　　　　　　 ●●
　　　　　　　　　　　　　　　     ４×２

　　　　８＝２×４　　　　　　　　８＝４×２
　　　　　＝２×２×２　　　　　　 ＝２×２×２　　となり、
　　　　けっきょくどちらも同じになります。

■　９　は素数ではありません。

　　　　　　●●●　　とならべられます。
　　　　　　●●●
　　　　　　●●●
　　　　　　　３×３

■　１０　は素数ではありません。

　　　　　　●●●●●　　や　　●●　のようにならべられます。
　　　　　　●●●●●　　　　　 ●●
　　　　　　　　２×５　　　　　　　 ●●
　　　　　　　　　　　　　　　　　　　●●
　　　　　　　　　　　　　　　　　　　●●
　　　　　　　　　　　　　　　　　　　５×２

　　　　　　１０＝２×５　も　１０＝２×５　もかける順番をのぞけば同じです。

■　１１　は素数です。

　　　　　　●●●●●●●●●●●　も　●　も１列です。
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●
　　　　　　　　　　　　　　　　　　　　　　　　　●

■　１２　は素数ではありません。

　　　　　　●●●●●●　　や　　●●　や
　　　　　　●●●●●●　　　　　 ●●
　　　　　　　　　２×６　　　　　　　　●●
　　　　　　　　　　　　　　　　　　　　 ●●
　　　　　　　　　　　　　　　　　　　　 ●●
　　　　　　　　　　　　　　　　　　　　 ●●
　　　　　　　　　　　　　　　　　　　　　６×２

　　　　　　●●●●　　や　　●●●　のようにならべられます。
　　　　　　●●●●　　　　　 ●●●
　　　　　　●●●●　　　　　 ●●●
　　　　　　　　３×４　　　　　　●●●
　　　　　　　　　　　　　　　     　４×３

　　　　１２＝２×６　　　　　　　　１２＝６×２
　　　　　　＝２×２×３　　　　　　 　＝２×３×２　　

　　　　１２＝３×４　　　　　　　　１２＝４×３
　　　　　　＝３×２×２　　　　　　　 ＝２×２×３　

　　　　となり、どれもかける順番をのぞけば同じになります。

●　素因数分解　●

　さて、ここで一休みしましょう。

　１２＝２×２×３　のように、素数のかけ算の形にすることを
素因数分解（そいんすうぶんかい）といいます。

　そして、いままでみてきたように、素因数分解は順番をのぞいて１通りです。
　（本当は証明しないといけませんが・・・）

　でも、もし　１　も素数ということにしていたら

　　　　１２＝２×２×３×１×１×１

というように、いろいろな素因数分解がでてきて、ややこしくなるところでしたね。
　もっとも、整数というからには負の整数もあるから

　　　　１２＝（−２）×（−２）×３

といような別の分解もあるのでは・・・？
　その対策もちゃ〜んと考えてあって、

　　　１　と　−１　は特別な数で

これらをかけ算していっしょになったら同じと考えよう、というものです。

　つまり、　２　と　−２　は同じとみなすのですから、

　　　　１２＝　　２　×　　２　×３

　　　　１２＝（−２）×（−２）×３

も、もちろん同じ分解とみなすのです。

　つまり、ど〜しても素因数分解は１通りであってほしい、という願いが先にあって
もろもろの理由づけは後のことなのです。

　では、どうしてそんなに素因数分解は１通りであってほしいのでしょうか。

●　因数分解　●

　因数分解って知っていますか。（中学でやります）

　　　　（Ｘ＋２）（Ｘ＋３）　＝　Ｘ^２＋５Ｘ＋６

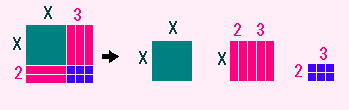
のようにバラバラにすることを展開といいます。
　その反対で、

　　　　Ｘ^２＋５Ｘ＋６　＝　（Ｘ＋２）（Ｘ＋３）

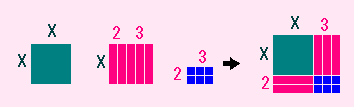
のように、バラバラなのをくっつける方を因数分解というのです。
　くっつけるのに分解というのは変・・・と思われるかもしれませんが
Ｘ^２＋５Ｘ＋６　という２次式を　Ｘ＋２　や　Ｘ＋３　のような１次式に分解しているわけです。

　数でいうなら、
　　　　２×２×３＝１２　のかけ算の方が　展開で
　　　　１２＝２×２×３　の素因数分解の方が　因数分解にあたります。

　で、どちらがかんたんですか？

　　　展開　と　因数分解　と　・・・
　　　かけ算　と　素因数分解　と　・・・

　もちろん、展開やかけ算ですよね。

　でも、こんなことがコンピュータ関係で話題の「暗号」のもとになっているのです。
　暗号をつくるのに大きな素数を２つかけた数、つまりかけ算をつかうと、
これを解読するには何と何をかけたのか、つまり素因数分解しなくてはならなくなり
と〜ってもむずかしいというわけです。

●　約数　●

　「divide」　,　「division」　,　「divisor」　の意味がわかりますか？（英語です）

　じゅんに、「わる」「わり算」「約数（やくすう）、除数（じょすう）」という意味です。
ちなみに、除数（じょすう）というのは、「わる数」のことです。
　たとえば、

　　　　１２÷３＝４

のとき、３でわるのですから、３が除数です。
　そして、３を１２の約数（やくすう）といいます。

　英語で勉強していたら、約数というのはわり算と関係あり！って
すぐにそうぞうがつきますね。

　そして、この約数がパッと見ただけでわかるのが、
なんと素因数分解というわけです。

　そこで、素因数分解を　１２　で、もう一度やってみましょう。

　まず、１２　をみて頭の中でかけ算の九九をとなえます。
　すると、２×６＝１２　がうかびます。（　３×４＝１２　でもいいですよ）
　かけ算の反対はわり算ですから、これは　１２÷２＝６　ということです。

　　　　１２÷２＝６　　を　　２）１２
　　　　　　　　　　　　　　　　　　  ６

と書いて、さらに今度は　６　をみて続けます。

　　　　　６÷２＝３　　を　　２）　６
　　　　　　　　　　　　　　　　　　　３

と書きます。３は素数ですから、これでおしまい。
　これを、続けてやると次のようになります。

　　　　２）１２
　　　　２）　６
　　　　　　　３

　これから、１２の素因数分解は

　　　　１２＝２×２×３

となります。
　ここまでやってきたことを考えると、１２　が　２　や　３　でわり切れるのは
当然・・・って感じですよね。
　つまり、２　や　３　が　１２　の約数ってことは、まあ当然かな〜って思えます。

　でも、１２　の約数がこれで全部わかるといったら、ちょっとおどろきでしょ。
　じつは、１２の約数は、これらの　２，２，３　を使ってかけてできる数なのです。

　　　　２，２，３　のうち　どれも使わないのが　１
　　　　２，２，３　のうち　２　だけ使うと　２
　　　　２，２，３　のうち　３　だけ使うと　３
　　　　２，２，３　のうち　２と２　を使うと　２×２＝４
　　　　２，２，３　のうち　２と３　を使うと　２×３＝６
　　　　２，２，３　のうち　２と２と３　を使うと　２×２×３＝１２

　１２の約数は　１，２，３，４，６，１２　です。

　・・・ということは、

　　　　１２＝２×２×３

という素因数分解を見ただけで、こんなこともわかるということです。

　１２　は　２×２＝４　ではわりきれるけど、２×２×２＝８　ではわりきれない。
　１２　は　３　ではわりきれるけど、３×３＝９　ではわりきれない。
　１２　は　５　や　７　では（最初から）わりきれない。

　さっき、こんなことを言いましたね。

　ど〜しても素因数分解は１通りであってほしい、という願いがまずあるのですが、
では、どうしてそんなに素因数分解は１通りであってほしいのでしょうか。

　もう、わかりましたね。

　わりきれる、わりきれない・・・ということを使って話を進めようとしているのに

　　　　１２＝２×２×３
　　　　１２＝２×３×３　（もちろんデタラメ）

と２通りに素因数分解されたらどうでしょう。

　　　　１２＝２×２×３

となったので、１２　は　３×３＝９　でわりきれない　と考え、
このことを使ってある定理を証明したと思っていたら、

　　　　１２＝２×３×３　（もちろんデタラメ）

とも素因数分解できることがわかって、
１２　は　３×３＝９　でわりきれる　となってしまい、
あのときの証明はいったい何だったのだろう・・・
と、こんな変なことになってしまいます。

　じつは、ある数学者がもっとむずかしいお話で、
こんなまちがいをしでかすところでした。
　その数学者は、自分でまちがいに気づきましたが、
やはり、ど〜しても素因数分解は１通りであってほしい、という願いから
一見ちがっている素因数分解を同じとみなす理由づけを考え出しました。

●　わり算　●

　因数分解は中学校でやるのに、なぜかわり算は高校になってから・・・
というわけで、因数分解とわり算がむすびつかない人が多いようです。

　では、やってみましょう。

　　　　Ｘ^２＋５Ｘ＋６　＝　（Ｘ＋２）（Ｘ＋３）

　これからわかることは、

　　　　Ｘ^２＋５Ｘ＋６　は　Ｘ＋２　でわりきれる。
　　　　Ｘ^２＋５Ｘ＋６　は　Ｘ＋３　でわりきれる。

　さらには

　　　　Ｘ^２＋５Ｘ＋６　は　Ｘ＋１　でわりきれない。
　　　　Ｘ^２＋５Ｘ＋６　は　Ｘ−２　でわりきれない。

　もちろん、

　　　　１２＝３×４　　から　　１２÷３＝４

であることがわかるように、

　Ｘ^２＋５Ｘ＋６　＝　（Ｘ＋２）（Ｘ＋３）　から　（Ｘ^２＋５Ｘ＋６）÷（Ｘ＋２）＝Ｘ＋３

であることがわかります。
　でも、いちおう（高校でやる）筆算でやってみましょう。

　　　　　　　　Ｘ　＋３　　　　
　　　　Ｘ＋２）Ｘ^２＋５Ｘ＋６
　　　　　　　　Ｘ^２＋２Ｘ　　　
　　　　　　　　　　　３Ｘ＋６
　　　　　　　　　　　３Ｘ＋６
　　　　　　　　　　　　　　 ０

　計算のやりかたは、ふつうのわり算とほとんどかわりませんね。

　さて、もうわかった人も多いでしょうが、

　　　　Ｘ^２＋５Ｘ＋６　は　数でいうと　合成数のようなもの
　　　　Ｘ＋２　や　Ｘ＋３　は　数でいうと　素数のようなものです。

　しかし、素因数分解や因数分解ができるはずということと、
（あなたやわたしが）じっさいに素因数分解や因数分解ができることとは話がべつです。
　もしそんな才能があったら、暗号の解読に大かつやく・・・かも。

HOME（もどる）

掲載内容の無断転載、転用、編集を禁じます。(c) 小林吹代
All Rights Reserved, （c）kobayashi fukiyo , 2001