多項定理
● パスカルの三角形 ●
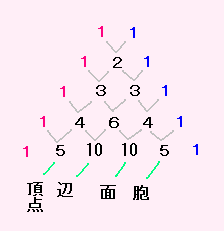
パスカルの三角形には、
「三角形」の頂点や辺や面の個数がひそんでいました。
(このホームページの「4次元」でやりましたね。)
|
1 2 1 |
|
2 は頂点の個数 |
|
1 3 3 1 |
|
3 は頂点の個数
3 は辺の個数 |
|
1 4 6 4 1 |
|
4 は頂点の個数
6 は辺の個数 4 は面の個数 |
そして、4次元の三角形である正5胞体では・・・
1 5 10 10 5 1
5個の頂点、10個の辺、10個の面、そして5個の胞がありました。
● パスカル風三角形 ●
だったら、超立方体の頂点や辺の個数も
パスカルの三角形のように、パッと出てくるといいですね。
それなら、今度こそパスカルの三角形でなくって、
パスカルの正方形だろうって?
ざんねんでした。
やっぱり、「三角形」なのです。
しいていうなら、パスカル風三角形です。
(パスカル風なんて、なんだかおいしいお料理が出てきそうですね。)
下の表が、「正方形」「立方体」そして「超立方体」用の
パスカル風三角形です。

|
2 1 |
|
2 は頂点の個数 |
|
4 4 1 |
|
4 は頂点の個数 4 は辺の個数 |
|
8 12 6 1 |
|
8 は頂点の個数 12 は辺の個数 6 は面の個数 |
そして、4次元の正方形である超立方体(正8胞体)では・・・
16 32 24 8 1
16個の頂点、32個の辺、24個の面、そして8個の胞がありました。
● 2項定理 ●
パスカルの三角形といったら・・・、2項定理ですね。
(a+b)1 = 1a + 1b
(a+b)2 = 1a2 + 2ab + 1b2
(a+b)3 = 1a3 + 3a2b + 3ab2 + 1b3
(a+b)4 = 1a4 + 4a3b + 6a2b2 + 4ab3 + 1b4
(a+b)5 = 1a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + 1b5
そうそう、展開(てんかい)したときの係数に
頂点や辺の個数が出てきたのです。
だったら、「正方形」や「立方体」や「超立方体」の頂点や辺の個数だって、
何かの式を展開して出てこないかな〜って思いますよね。
それはもう、さっきのパスカル風三角形を
じ〜っとながめれば、すぐに出てくるというものです。
でも、せっかくですから、ちょっとまわり道してみましょう。
● 3次元のパスカルの三角形 ●
このホームページの「パスカルの三角形」を見ていただけましたか。
そこでは、碁盤(ごばん)の目のような道で、
行き方が何通りあるかを考えましたね。
だったら、これを2次元の平面でなくって、
3次元の空間にしたらどうなるでしょう。
さしずめ、3次元のパスカルの三角形ですね。
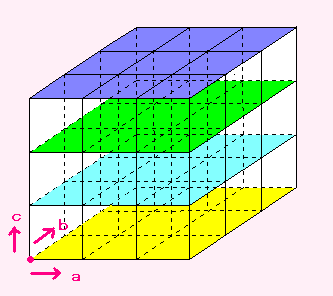
さて、それぞれの頂点にたどりつく方法は、
何通りあるかを書いていきましょう。
でも、この図に書きこむと、読めなくなってしまいそうです。
そこで、ちょうど建物(たてもの)の設計図(せっけいず)のように、
1階、2階、3階・・・のように、書いていくことにしましょう。
でも、ちょっとふつうとかえて、
0階からということにしましょう。
こうすると、0階はcの0乗、1階はcの1乗、2階はcの2乗・・・
となって、つごうがいいのです。
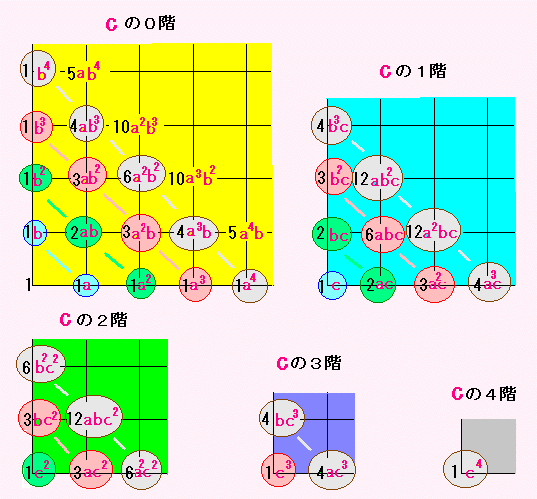
今度は、下の階から上がってくる方法も
わすれずにたし算しましょう。
もちろん、0階はふつうのパスカルの三角形になっていますね。
えっ、今度は a や b がついているって?
今回はややこしいので、2項定理いえ3項定理をみこして
最初からつけておいただけです。
さて、表ができたところで、「パスカルの三角形」でやったように、
(小さい立方体の一辺を1歩として)
1歩でいけるところ、2歩でいけるところ、3歩でいけるところ・・・
を考えてみましょう。
そんなところがどこか、すぐにわかりますよね。
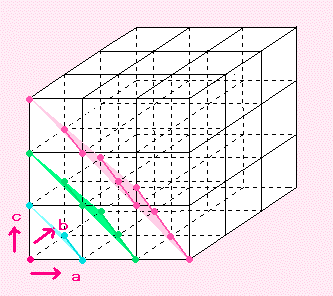
あとは、「パスカルの三角形」でやったのと同じようにして
次の3項定理(じつは、ただの展開)がでてきます。
(a+b+c)1 = 1a+1b
+1c
(a+b+c)2 = 1a2+2ab+1b2
+2ac+2bc
+1c2
(a+b+c)3 = 1a3+3a2b+3ab2+1b3
+3a2c+6abc+3b2c
+3ac2+3bc2
+1c3
(a+b+c)4 = 1a4+4a3b+6a2b2+4ab3+1b4
+4a3c+12a2bc+12ab2c+4b3c
+6a2c2+12abc2+6b2c2
+4ac3+4bc3
+1c4
● 超立方体 ●
さて、上の3項定理で、a=b としてみましょう。
(2a+c)1 = 2a+1c
(2a+c)2 = 4a2+4ac+1c2
(2a+c)3 = 8a3+12a2c+6ac2+1c3
(2a+c)4 = 16a4+32a3c+24a2c2+8ac3+1c4
これらの式を展開したら、ちゃ〜んと
「正方形」や「立方体」や「超立方体」の頂点や辺の個数がでてきましたね。
でも、こんなのパスカル風三角形をじ〜っとながめたら、
すぐにわかったことですよね。
そして、さらに2項定理までもどると・・・
(a+b)1 = 1a + 1b
(a+b)2 = 1a2 + 2ab + 1b2
(a+b)3 = 1a3 + 3a2b + 3ab2 + 1b3
(a+b)4 = 1a4 + 4a3b + 6a2b2 + 4ab3 + 1b4
ここで、 a=2 , b=−1 を入れてみましょう。
1 = 2 − 1
1 = 4 − 4 +1
1 = 8 − 12 + 6 −1
1 = 16 − 32 + 24 − 8 + 1
そしてこれより、
4 − 4 = 0
8 − 12 + 6 = 2
16 − 32 + 24 − 8 = 0
これは、「正方形」や「立方体」や「超立方体」でも、
このホームページの「4次元」でやった(じつは、とばした?)
次の式がなりたっているということですね。
|
|
えっ、2項定理でいいのなら、
いままで何をしてきたのだろうって?(まあ、い〜じゃないの)
とりあえず、こんなふうにして、何次元の立方体でも、
かんたんに頂点や辺の個数がかぞえられそうですね。
● 多項定理 ●
じつは、3項定理なんて、だ〜れもいわないのです。
(もちろん、3次元のパスカルの三角形なんていうのも・・・)
2項定理の次は、いきなり多項定理(たこうていり)なのです。
そして、これは高校のお勉強なのです。
|
(a+b+c+・・・)n の展開式の一般項は n! ( p+q+r+・・・=n , p,q,r・・・≧0 )
|
これは、3次元よりもっと高い次元のパスカルの三角形を使う・・・
はずがありません。
たんに、展開して同類項がいくつあるか数えるだけです。
たとえば、(a+b+c)4 を展開すると、
a2bc の係数が12、つまり+12a2bc がでてくるということは、
「パスカルの三角形」でやったように、
a,a,b,c のならべ方が
aabc , aacb ,abac , abca ,acab ,acba ,
baac , baca ,bcaa , caab ,caba ,cbaa ,
のように、12通り あるということです。
そして、そのa,a,b,c のならべ方が何通りあるかというのが、
4!
---------- (通り)
2!1!1!
で計算できるというのです。
ここで、4 というのは (a+b+c)4 の 4
2,1,1 は a2bc つまり a2b1c1 の 2,1,1 です。
そして、「!」は階乗(かいじょう)といって、
4!=4×3×2×1=24
のように、1ずつへらしながら1になるまでかけ算する記号です。
これはちょうど、ことなる4つのものを4つともならべる方法になっています。
ところが、a,a,b,c のならべ方は、a,a,と同じものがあるので、
これよりへります。
何分の1にへるかと考えることによって、
4!
---------- (通り)
2!1!1!
とすぐにでてくるのです。
そして、これを計算すると
4! 4・3・2・1
---------- = ---------- = 12
2!1!1! 2・1・1・1
と、ちゃ〜んと 12 とでてきます。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001