正多面体

●　ペンタグラム　●

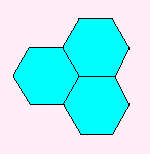
　ペンタグラムをみていたら、正五角形のまわりに５つの正五角形
つまり、全部で６つの正五角形がでてきました。

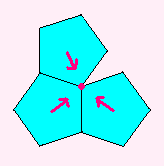
　そこで、こんなのを２枚用意して、
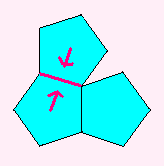
ちょっと切り取って、おりまげて、くっつけると
あらあら正１２面体のできあがりです。

　どの面も同じ正多角形でできている立体を、
正多面体（せいためんたい）といいます。

　正多面体が５種類、つまり

しかないことは、古くから知られていました。

　どうして５種類しかないのか知っていますか。

　じつは、やってみればすぐわかるのです。

　これらの多面体の面となる正多角形ですが、

　　　　　正３角形でできているのが、正４面体、正８面体、正２０面体
　　　　　正４角形（つまり正方形）でできているのが、正６面体
　　　　　正５角形でできているのが、正１２面体

と、なっています。

●　正多面体　●

＜正３角形＞

　では、まず正３角形を使ってできる正多面体からみていきましょう。

　１つの頂点のまわりに何枚使うか考えます。
　（じっさいに作ってみるといいですね。）

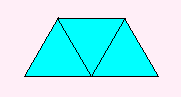
　１つの頂点のまわりに３枚使ってできるのが、正４面体です。

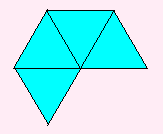
　１つの頂点のまわりに４枚使ってできるのが、正８面体です。

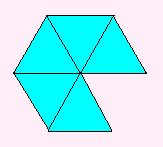
　１つの頂点のまわりに５枚使ってできるのが、正２０面体です。

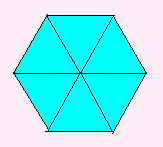
　１つの頂点のまわりに６枚使って・・・あらあら、ぺったんこ（たいら）になってしまいました。

　もちろん、７枚以上使ったら、ぺったんこどころか重なってしまいますね。

＜正４角形（正方形）＞

　では、次に正４角形（正方形）を使ってできる正多面体をみていきましょう。

　同じようにして、１つの頂点のまわりに何枚使うかで考えていきます。

　１つの頂点のまわりに３枚使ってできるのが、正６面体（立方体）です。

　１つの頂点のまわりに４枚使って・・・これは、ぺったんこ（たいら）でむりです。

　もちろん、５枚以上使って作るのはむりですね。

＜正５角形＞

　では、次に正５角形を使ってできる正多面体をみていきましょう。

　また、１つの頂点のまわりに何枚使うかで考えていきます。

　１つの頂点のまわりに３枚使ってできるのが、正１２面体です。

　４枚以上使ったら、ぺったんこどころか重なってしまってできませんね。

＜正６角形＞

　では、次に正６角形を使ってできる正多面体をみていきましょう。

　またまた、１つの頂点のまわりに何枚使うかで考えていくのですが、
なんと、１つの頂点のまわりに３枚使って・・・というところで、
はやくもむりですね。

　もちろん、正７角形からさきも、さいしょからむりというものです。

　こうして、正多面体は、できたとしても
今まで見てきた５種類だけとわかりましたが、
じっさい作ってみれば、ちゃ〜んと（？）５種類あるとわかりますね。

●　数える　●

　このホームページで、
数をかぞえる時に大切なことをやりました。

　おぼえていますか。

　それは、
「数え落としをしない」ということと
「おなじものを、二度かぞえない」ということでした。

　それでは、正多面体でかぞえてみましょう。

　何をかぞえるのかって？

　面の個数はわかっているものとして（・・・あとでやるってことにして）
頂点の個数と辺の個数をかぞえてみるのです。

　たとえば、正１２面体なら、
１つの頂点のまわりに正５角形を３枚使って作っていったら
何枚でできるか・・・ということは、ちょっとおいておいて
とりあえず１２枚でできたということから話をはじめるのです。

　まず、頂点ですが、
正５角形には５つの頂点がありますから、１２枚だと

　　　　　５×１２＝６０　（個）　

の頂点があるといったら、大ウソです。

　そうです。「おなじものを、二度かぞえない」はずが、
３度もかぞえてしまっているからです。

　でも、どの頂点もきっちり３度かぞえているので話はかんたんです。
３でわればいいだけです。

　同じようにして、辺なら２でわればいいだけですね。

　それでは、のこしておいた、

　１つの頂点のまわりに正５角形を３枚使って作っていったら
　何枚でできるのか。

　・・・という答えが、どうして１２枚ってきまってしまうのでしょうか。

　それはまた今度、ということで・・・とりあえずおしまい。

HOME（もどる）

掲載内容の無断転載、転用、編集を禁じます。(c) 小林吹代
All Rights Reserved, （c）kobayashi fukiyo , 2001