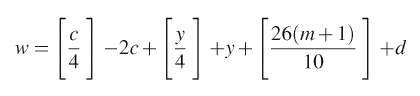何曜日?
● あなたの誕生日は何曜日? ●
自分の誕生日は何曜日か知っていますか?
そんなの母子健康手帳に書いてあるよ
っていう人、うらやましい!
なんでかって?
昔はそんなのなくって
何曜日かまではおぼえていてもらえなかったからです。
ある日、おもしろい「下じき」が手にはいりました。
表があるタレントさんの写真で
うらが「万年カレンダー」というものです。
今はなくしてしまってありませんが
自分の誕生日が月曜日だったことは
しっかり覚えています。
それから何年かたって、こんな公式を見つけました。
1921年にアメリカのPrinceton大学のPhilip Franklin
という人が
求めた公式だそうです。
ただし、[ ]はガウスの記号とよばれるもので、 c は 西暦年数の上2けた w を 7 でわったあまりによって
|
● やってみよう! ●
では、Javaアプレットでやってみましょう。
半角の数字を入れてやってみてね。
ファイル名の不備により、現在classファイルが
アップされていません。(すみません!)
● あまりはいくつ? ●
さて、これでおしまいのはずありませんね。
いよいよ、さんすう・数学のお勉強です。
この公式を求めてみようなんて、も〜ちろん、言いません。
w は 正の数のときもありますが、負の数のときもあります。
ところで、負の数のときのあまりの求め方知っていますか?
たとえば、(−25)÷7 のあまりはいくつでしょうか。
あまりのあるわり算は、小学校のときしかやらないし
負の数は中学校でやるので、けっきょくどこでも勉強しなかった・・・かな。
それでは、せっかく公式を教えてもらっても、
あまりが出せなくて、宝のもちぐさりになってしまいます。
(−25)÷7 = (−3) あまり −4
ではありませんよ。
あまりはわる数より小さい、のほかにもう1つ習いましたね。
あまり というくらいですから たりない ではこまります。
あまりは 0以上 でした!
(−25)÷7 = (−4) あまり 3
となります。えっ、それくらい知っていたって。
そうですよね〜。
● 暦の歴史 ●
さて、この公式には暦の歴史がでています。
まず、最初にローマで暦が作られたときは、
1年は3月から始まって12月でおしまい、つまり1年は10ヶ月で
のこりの2ヶ月間は農作業をしないお休みの日だったそうです。
それから、1月と2月がつけくわわって全部で12ヶ月となりました。
3月から始まって2月までです。
3月(31日)、4月(30日)、5月(31日)、6月(30日)、
7月(31日)、8月(30日)、9月(31日)、10月(30日)
11月(31日)、12月(30日)、1月(31日)、2月(29日か30日)
これがユリウス暦というもので1月から始まることにしました。
(うるう年は4年に1度です)
1月(31日)、2月(29日か30日)、3月(31日)、4月(30日)
5月(31日)、6月(30日)、7月(31日)、8月(30日)
9月(31日)、10月(30日)、11月(31日)、12月(30日)
ところが、皇帝アウグストゥスが自分の誕生日の8月を31日にして
そこから30日と31日を反対にしてしまいました。
この関係で、2月がさらに1日へりました。
1月(31日)、2月(28日か29日)、3月(31日)、4月(30日)
5月(31日)、6月(30日)、7月(31日)、8月(31日)
9月(30日)、10月(31日)、11月(30日)、12月(31日)
ローマ法王グレゴリウス13世は、次のように誤差の調整をしました。
これがグレゴリウス暦です。
・100で割り切れる年は平年
・400で割り切れる年はうるう年
ちなみに、2000年問題で話題になった昨年は
2000÷4=500 で うるう年のはずでしたが
2000÷100=20 で やっぱり平年になるはずでしたが
2000÷400=5 で 結局うるう年でした。
ちょっとした話題になってましたね。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001