わりきれる？わりきれない？　～さんすう・数学のお勉強～

わりきれる？

●　分数を小数になおす　●

　　　ケーキだ～いすき！
　　　　　　　　　　　まるごと１個食べたいな！！
　　　　　　　　　　　　（分数なんて・・・・・）

　１/２＝１÷２＝０．５

　１/３＝１÷３＝０．３３３３３・・・・・

　１/４＝１÷４＝０．２５

　１/５＝１÷５＝０．２

　１/６＝１÷６＝０．１６６６６・・・・・

　１/７＝１/７＝１÷７＝０．１４２８５７１４２８５７・・・・・

　１/８＝１÷８＝０．１２５

　１/９＝１÷９＝０．１１１１１・・・・・

　１/１０＝１÷１０＝０．１

　１/１１＝１÷１１＝０．０９０９０９０・・・・・

　１/１２＝１÷１２＝０．０８３３３３・・・・・

　１/１３＝１÷１３＝０．０７６９２３０７６９２３０・・・・・

　で、いったいどのようなときに割りきれるの？

　このようなとき、ず～っとやってみて、
何かみつけるというのは大事なことです。

　でも、基本にもどって
何が問題になっているのかをハッキリさせることは
もっと大事なこと。

　いまの場合では、たとえば
　　　１/８＝１÷８＝０．１２５
で、１/８　は　１を８等分した１つ分ですが、これが
０．１　と　０．０２　と　０．００５
をあわせたもの、つまり
　　　１を１０等分した１つ分と
　　　１を１００等分した２つ分と
　　　１を１０００等分した５つ分に
キッチリなった。

　それはなぜか？

　そして、１/３　は　１を３等分した１つ分ですが
　　　１/３＝１÷３＝０．３３３３３・・・・・
となるということは、
　　　１を１０等分した３つ分と
　　　１を１００等分した３つ分と
　　　１を１０００等分した３つ分と
　　　・・・・・・・・・・・・・・・・・・・・・・・
といくら続けても、いつまでもチリのように
かすかにあまってくる。

　これはなぜか？

●　１０進法　●

　さて、小数って、１０等分、１００等分、１０００等分
してあらわす数でした。
　もちろん、１００等分というのは、
１０等分のさらに１０等分。
　１０００等分というのは、
１０等分の１０等分のさらに１０等分です。

　そう、人間の両手の指の数　１０　です。

　なんで、そんなにしつこく指の数にまで話をもどすの？
と思いますか。

　それは、この問題は
数を１０進法であらわすことから生じた問題で、
もし、指の数が両手で１２本だったら、
また、かわってくるだろうな～ということだけは
おさえておきたかったからです。

●　素因数分解　●

　さて、話をもとにもどして
　　　１/８＝１÷８＝０．１２５
を、筆算や電卓でなく、今度は分数の基本にもどって
考えてみましょう。

　１/８　は　１を８等分した１つ分です。
これを、さらに切りきざんで、
１０等分とか１００等分とか１０００等分されたものの
いくつ分かにしたいのです。

　もちろん、すでに８つに切られているものを、
さらに切りきざむのですよ。

　８つに切られているものを、さらに２つに切ると
　　　　８×２＝１６　に切れます。
　８つに切られているものを、さらに３つに切ると
　　　　８×３＝２４　に切れます。

　いくらなんでも、
　　　　８×（　）＝１０
のように、８等分から１０等分にはできないですよね。では、
　　　　８×（　）＝１００
のように、８等分から１００等分にはできるでしょうか。
それも、むりなのです。なぜなら、

　　　　８＝２×２×２

　　１００＝１０×１０
　　　　　＝２×５×２×５
　　　　　＝２×２×５×５

を使うと、（素因数分解といいます）

　　　　８×（　）＝１００

にしたいということは

　　　　２×２×２×（　）＝２×２×５×５

にしたいということですが、

　２×２×２に何かをかけた結果、２×２のように
２が１つへってしまうことはないからです。
（素因数分解の一意性を用いています）

　では、８等分から１０００等分にはできるでしょうか。
これは、できるのです。なぜなら、

　　１０００＝１０×１０×１０
　　　　　　＝２×５×２×５×２×５
　　　　　　＝２×２×２×５×５×５

を使うと、

　　　　２×２×２×（　）＝２×２×２×５×５×５

にするには、（　）の中の数は５×５×５、
つまり１２５にするとよいからです。

　８等分されたものを、さらに１２５等分すると
１０００等分にされるのです。

●　やってみよう！　●

　もう一度、分数の計算でやってみましょう。
約分は、分子と分母を同じ数でわることですが
今回はその逆で、分子と分母に同じ数をかけます。

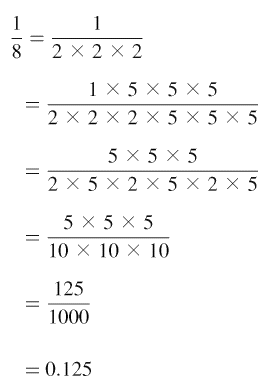
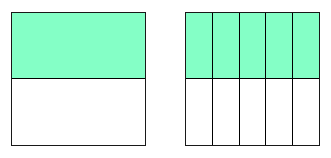
　では、１/２＝１÷２＝０．５　もこの方法で
やってみましょう。

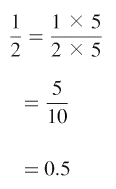　　　　　　１/２　　　　　　　　　　　　　５/１０

　しつこいようだけど、１/５＝１÷５＝０．２　も
やってみましょう。

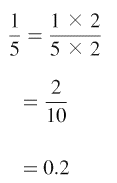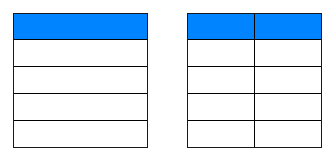　　　　　　１/５　　　　　　　　　　　　　２/１０

　だめおしに、１/４＝１÷４＝０．２５　も
やってしまいます。

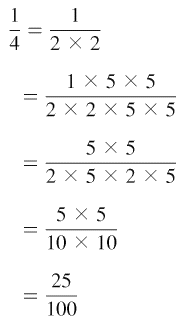
　　＝０．２５

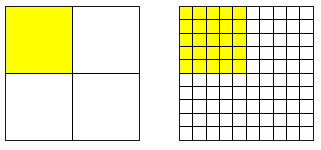　　　　　　１/４　　　　　　　　　　　　２５/１００

●　まとめ　●

　さいごに、まとめましょう。

　　１/２＝１÷２＝０．５
　　１/４＝１÷４＝０．２５
　　１/５＝１÷５＝０．２
　　１/８＝１÷８＝０．１２５
　　１/１０＝１÷１０＝０．１

などが割りきれるのは、
分母が２や５ばかりかけ算してできた数だからです。

　　１/３＝１÷３＝０．３３３３３・・・・・
　　１/６＝１÷６＝０．１６６６６・・・・・
　　１/７＝１/７＝１÷７＝０．１４２８５７１４２８５７・・・・・
　　１/９＝１÷９＝０．１１１１１・・・・・
　　１/１１＝１÷１１＝０．０９０９０９０・・・・・
　　１/１２＝１÷１２＝０．０８３３３３・・・・・
　　１/１３＝１÷１３＝０．０７６９２３０７６９２３０・・・・・

などが割りきれないのは、
分母が２や５ばかりかけ算してできた数ではない、
つまり２や５以外の数もかけられてできた数だからです

　もし、人間の両手の指の数が１０本でなかったら、
どうなるかも考えてみてね！！

HOME（もどる）