負の数×負の数　～さんすう・数学のお勉強～

負の数×負の数

●　負の数×負の数　●

　こんなメールをいただきました。

　

　・・・　私は今高校生なのですが、
「（負の数）×（負の数）＝（正の数）になるのは何故か、中学生にもわかるように説明しなさい。」

という宿題を出され　・・・

　おもしろい先生ですね～。

　どこがって？

　「中学生にもわかるように」ってとこですよ。

　だって、（負の数）×（負の数）＝（正の数）って
中学校のお勉強なのですから・・・。

　ですから、中学校の教科書を見れば
ちゃ～んと書いてあります。（たぶん、書いてあるはずです。）

　そこで、中学生向きの説明は今回はやめておいて
高校生向きにやってみましょう。

　もっとも、小学生むきになってしまうかもしれませんが・・・。

●　複素数　●

　このホームページの「ペンタグラム」で、ガウス平面というのをやりました。

　直線の上に数がのっかっているのが数直線なら、

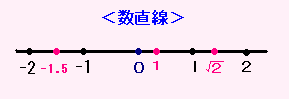
　平面の上に数がのっかっているのがガウス平面というものです。

　そして、たし算やかけ算の「おやくそく」をしました。
（もちろん、ひき算やわり算もその逆としてきまってきます。）

　かけ算すると、長さはかけた長さに、角度はあわせた角度にしたのです。
　（角度というのは実軸の正のところから、時計と反対まわりにはかった角度です。）

　それでは、

　　　　　（負の数）×（負の数）＝（正の数）になるのはなぜか

を、ガウス平面で考えてみましょう。

　たとえば、（－２）×（－３）で考えてみます。

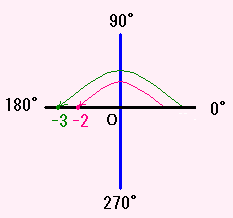
　ガウス平面では、（数直線でもいいですが・・・）

　　　　　－２　は　長さが　２　で角度が　１８０°のところにある数
　　　　　－３　は　長さが　３　で角度が　１８０°のところにある数

　すると、（－２）×（－３）　は

　　　　　長さが　２×３　で、
　　　　　角度が１８０°＋１８０°＝３６０°（つまり　０°）

のところにある数、つまり　６　です。

　けっきょく、

　　　　　（負の数）×（負の数）＝（正の数）になるのはなぜか

というと、１８０°＋１８０°＝３６０°（つまり　０°）　となるってこと、
つまり、半回転と半回転で１回転になってもとにもどるってことですね。

　でも、中学生はガウス平面なんてやらないので、
数直線で向きを考えて、

　　　　　反対向きの反対向きはもとの向き

なんて説明（？）したりもします。

　負の数のかけ算をどのように「おやくそく」するかで、
説明のしかたもかわりますから、
そこのところを気をつけて、いろいろ調べてみてくださいね。