0.999･･･はどうして1と等しいの？　～さんすう・数学のお勉強～

１と０．９９９・・・
どちらが大きい？

●　「・・・」の意味　●

　「１　と　０．９９９・・・　どちらが大きい？」

　こう聞かれたら、どう答えますか。
あ～でもない！こ～でもない！という人に
ちょっと聞いてみてください。

　「その前に、０．９９９・・・というのは、
どういう意味ですか」　と。
　そこのところを、ハッキリさせないと
話が始まらないですから　ね。

　「ええっ？　だって　０．９９９・・・って、０．９９９・・・でしょ？」

　そういうのが、こわいんですよ。
おもいこみっていうものです。

　だって、あなたが思っている　０．９９９・・・　と
わたしが思っている　０．９９９・・・　が
本当に、同じかどうかあやしいものです。

　だから、始めに「０．９９９・・・」の「・・・」のところを
あなたとわたしで、キッチリ取り決めておかないと、
あとで、そんなつもりでなかったとか
いろいろともめるもとなんです。

●　定義　●

　さんすう・数学では、そういう最初の取り決めを
定義（ていぎ）とよんでいます。

　じつは、０．９９９・・・の取り決めは
次のようにしています。

　０．９
　０．９９
　０．９９９
　０．９９９９
　０．９９９９９

　こういう数は、小学校の小数のお勉強で
ちゃんとやりましたね。
　そこで、このような数がどんな数に近づくかを考えて
その近づいていった先の数のことを
　０．９９９・・・
と書き表すことにしましょうというのです。

　そりゃ　１　に近づく・・・ようね。
　そこで、

　０．９
　０．９９
　０．９９９
　０．９９９９
　０．９９９９９

などは、いつまでたっても、もちろん　１　ではないし
たしかに　１　より小さいけれど

　０．９９９・・・

は、最初の取り決めで、その近づいていった先の数って
決めたのですから、１そのものなのです。

　ですから、
　　　０．９９９・・・＝１
ですね。

　ただし、本当に１に近づくかどうか　とか
そもそも、近づくとはどういうふうに取り決めるのか　とか
いろいろ疑問に感じることは、とっても大切なこと。
（このことは、高校や大学で勉強しますので
楽しみにしていてね。）

　それから、自分でいろいろ工夫して
取り決め方そのものを考えるのも、楽しいですね。
　それが、みんなに納得してもらえるものだったり、
とっても役に立つものだったら
もしかしたら、注目されるかもしれませんよ。

●　発展　●

　さて、練習をしてみましょう。
　下の式をみてね。　

　１　というのは、ここでは正方形の紙１枚のこと。
　２分の１はその半分、
４分の１はそのまた半分です。

　どんどん　１　にちかづくな～って、
絵をみればパッと（それがまちがいのもと？）分かるよね。

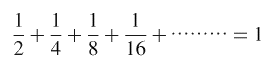
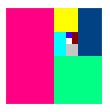
　でも、これって
　　　　０．９９９・・・＝１
と同じなんだなあ。

　どこが・・・って？

　もちろん、どっちも　１　だから
なんてことではないよ。

　そのうち　「お勉強」にのせるよてい！
それまでに、考えておいてね。