正方形への分割
● 正方形への分割 ●
大学3年生の方から、こんな質問のメールをいただきました。
ちょっと見るとクイズやパズルのようですが、じつは、さんすう・数学ともいえます。
そこで、問題の部分だけ、しょうかいさせていただきます。
|
【問題1】 2辺が47と65の長方形がある。 【問題2】 2辺が32と33の長方形がある。
|
これって、ユークリッドの互除法(ごじょほう)の練習問題です。
「ユークリッドの互除法」は、このホームページでも取り上げましたね。
● ユークリッドの互除法 ●
ユークリッドの互除法は、
おたがいに、わり算していくのでした。
くわしいせつめいは、<お勉強>の「ユークリッドの互除法」をみてください。
ここでは、けっかだけにしましょう。
【問題1】は、
2辺が47と65の長方形ですから、
47と65をおたがいにわり算していくのです。
65÷47=1 あまり 18
47÷18=2 あまり 11
18÷11=1 あまり 7
11÷7=1 あまり 4
7÷4=1 あまり 3
4÷3=1 あまり 1
3÷1=3
ここで、
1+2+1+1+1+1+3=10(個)
これを図にすると、つぎのようになります。
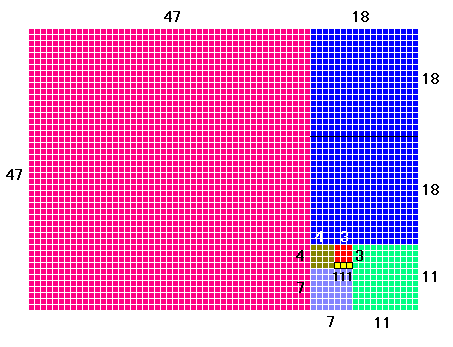
● 素因数分解 ●
もちろん、このような問題は、かならずユークリッドの互除法でできる・・・
なんて、だれもいっていません。
なにしろ、つかう正方形の個数がきめられているのですから。
何個でもいいのなら、ユークリッドの互除法でいいのですが・・・。
もっとも、何個でもいいのなら、
いつだって、1辺が1の正方形でしきつめればいいですよね。
さて、ユークリッドの互除法で、
すんなりいかないのが、【問題2】です。
【問題2】は、
2辺が32と33の長方形ですが、
32と33をおたがいにわり算していくと、
あっというまにおしまいです。
33÷32=1 あまり 1
32÷1=32
ここで、
1+32=33(個)
でも、問題は、9個の正方形でしきつめろといっているのです。
33個なんて、とんでもないですね。
そこで、ここからはパズルです。
つまり、いろいろやってみるのです。
・・・とはいっても、デタラメではうまくいきそうにもありません。
まずは、32と33という数について、みてみます。
それぞれの数の素因数分解は、つぎのようになります。
32=2×2×2×2×2
33=3×11
どうも、33がよさそうです。(こういうところがパズルです。)
33なら1辺が11の正方形が3個とれます。
そこで、その3個の正方形をとりのぞいて、
ユークリッドの互除法がつかえないかなとやってみるのです。
32−11=21
つまり、21と33でやってみるのです。
わかりにくいので、けっかの図をさきにのせてしまいます。
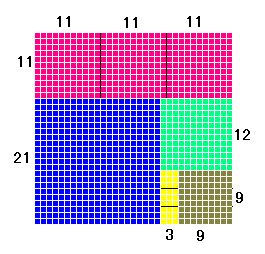
それでは、21と33をおたがいにわり算していきます。
33÷21=1 あまり 12
21÷12=1 あまり 9
12÷9=1 あまり 3
9÷3=3
ここで、さいしょの3個とあわせると
1+1+1+3+3=9(個)
ああ、うまく9個になったな〜ということで、おしまい。
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001