図形でピタゴラス数　～さんすう・数学のお勉強～

図形でピタゴラス数

●　自由研究　●

　最近、「夏休みの宿題ができてな～い。数学はこのホームページでやろう！」
というような、メールをいただきました。

　きっと、数学にも「自由研究」のようなものがあるのでしょうね。

　このメールは中学生の女の子でしたから、もしかしたら
「ピタゴラス数」は高校生向きだからやめておこうって思ったかもしれませんね。

　そこで、アドバイスをひとつ・・・。

　それは、（このホームページにかぎらず）、
ほかの方法でもできないかなってやってみることです。

　そうしたら、りっぱな自由研究になりますね。

●　ピタゴラス数　●

　＜お勉強＞の「ピタゴラス数」を読んでいただけましたか。

　あれは、グラフを使うものでしたが、
「解と係数の関係」で、そんなの知らな～いって人には・・・

　じつは、ほかにも初等整数論を使う方法もあるのですが
場合分けがあったりして・・・

　目からうろこといった感じのものでは、代数的整数論を使う方法があるけど
そこに行き着くまでに・・・。

　そこで、今回は中学生向きに図形でやってみました。

　こんなことが、問題になっていましたね。

　X　と　Y　を　ｔ　をつかってあらわそうというのです。

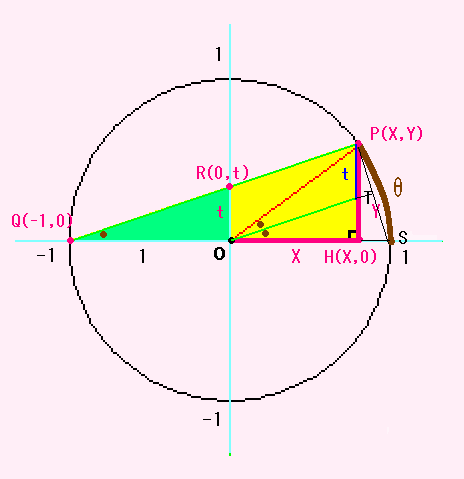
　今回はこの図から、円を消してしまいます。

　まず、そのために角POHの二等分線をOTとします。

　四角形ROTPは平行四辺形となって、
ROの長さｔ　は　PTの長さと等しいことに気づきます。

　そこで　ｔ　は　これからPTの長さとします。

●　初等幾何　●

　さて、X　と　Y　を　ｔ　を用いてあらわしてみましょう。

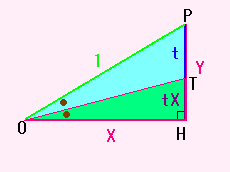
　まず、直線OTは角POHの二等分線ですから

　　　　　PT　：　TH　＝　１　：　X

となりますから、TP＝ｔ　なので

　　　　　TH＝ｔX

　次に、点Pから直線OT（の延長線）へ垂線PUをおろして、
直線OH（の延長線）との交点を　S　とします。

　そうすると、三角形POU　と　三角形SOU　は合同ですから

　　　　　OS＝１　

がわかります。さらに、

　　　　　HS＝１－X

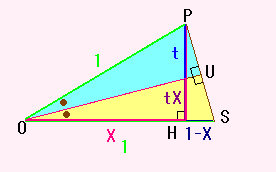
　さらに、角TOH　と　角TPU　が等しいことに注意すると
三角形TOH　と　三角形SPH　が相似であることがわかります。

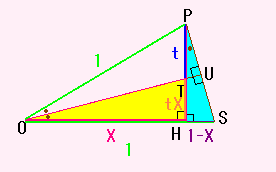
　そこで、

　　　　　OH　：　TH　＝　PH　：　HS

　　　　　　X　：　ｔX　＝　（ｔ＋ｔX）　：　１－X

　　　　　　１　：　ｔ　　＝　ｔ（１＋X）　：　１－X

　　　　　　ｔ^２（１＋X）　＝　１－X

　　　　　　ｔ^２　＋　ｔ^２X　＝　１－X

　　　　　　ｔ^２X　＋　X　＝　１－ｔ^２　

　　　　　（　ｔ^２　＋１）X　　＝１－ｔ^２

　　　　　　　　　　　　　　　　１－ｔ^２
　　　　　　　　　　　　^X　＝　１＋ｔ^２　

さて、今度は　Y　ですね。

　　　　　Y　＝　ｔ　＋ｔX　

　　　　　Y　＝　ｔ（１＋　X）

　　　　　　　　　　　　　　　　１－ｔ^２
　　　　　^{Ｙ　＝　ｔ（１　＋}　１＋ｔ^２　^）

　　　　　　　　　　　　２ｔ　　
　　　　　^Ｙ　＝　１＋ｔ^２　

　ですから、＜お勉強＞の「ピタゴラス数」とあとのお話はいっしょになりますね。

　じつをいうと、わたしは幾何って初等幾何さえもにがてなのですが、
今回は前に円でやったので、補助線がそのまま使えて、
”ひらめき”を必要としませんでしたね。

HOME（もどる）