質問(連分数)
● 質問 ●
こんなメールをいただきました。
|
連分数とはどんな数なのですか
|
う〜ん!
そうなんですよね〜っ!!
まずは、そこから話をはじめるべきなんですよね。
それで、さっそく連分数(れんぶんすう)の定義(ていぎ)
つまり、連分数ってこんなものだよ〜っていうお約束を書けばいいのですが、
じつは、いろいろややこしいのです。
収束(しゅうそく)の問題とかもあって・・・。
もちろん、ちゃんとした数学の本では、
そこから話をはじめています。
でも、そもそも連分数なんて、
小学校や中学校でお勉強するようなことではないのです。
高校でさえもありません。
ということは・・・?
そう、大学です!
じつは、このホームページには
やさしそうに見えて、大学のお勉強も入っているのです。
でも、せっかくの質問ですから、
ちょっと考えてみることにしましょう。
● 小数と分数 ●
では、小学生になったつもりで考えてみてください。
まず、小数って、どんな数でしょう?
う〜ん、1より小さい数かな。
いえいえ、1.4 も 3.14 も1より大きいけれど、りっぱな(?)小数です。
それなら、・・・−3,−2,−1,0,1,2,3,・・・のように、(これらは整数ですね)
0から1ずつふやしたりへらしたりして、でてこない数かな。
ふ〜ん、それなら分数は?
分数だって、 ・・・−3,−2,−1,0,1,2,3,・・・のように、
0から1ずつふやしたりへらしたりして、でてこない数ですよね。
それに、小数と分数って、べつべつの数でなくって
1/4 = 0.25
のように、同じ数をちがったふうに書いただけですよね。
でも、1/3 は分数では書けるけれど、小数では書けないって?
そんなことは、ありません。
ちゃんと無限小数(むげんしょうすう)をつかって
1/3 = 0.3333333・・・・・・
と書けます。
● 長さ ●
小学生のときから、数をお勉強するたびに、
その数を、数直線(すうちょくせん)にあらわしてきました。
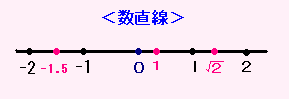
そう、数といったら長さをあらわすものなのです。
(負の数では向きも考えます。)
数があるのに、その数の長さがないとか
長さがあるのに、その長さの数がないというのでは
こまってしまいますからね。
ですから、正方形の対角線(たいかくせん)の長さの数もあるし
円の周りの長さの数もあるわけです。
もっとも、そんな数にいちいち名前をつけていたら
たまったものではありません。
わたしの身長は162、5cmよ!(まっかなウソです)
といってみても、それはあくまでも近いめもりを読みとっただけなのです。
わたしの身長をあらわす数だって、ちゃんとあるのですが、
名前がついていないだけなのです。
そして、近い小数でまんぞくしています。
名前がつけてもらえる数は、とくべつなものだけです。
無限にあるうちの、ほんのわずかです。
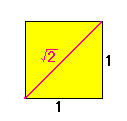
たとえば、1辺が1の正方形の対角線の長さは
1.41421356・・・・・・
ですが、これには /2 という名前がついています。
たとえば、直径が1の円周の長さは
3.14159265358979・・・・
ですが、これには π という名前がついています。

● 連分数 ●
さて、このホームページの「142857」でこんな数がでてきましたね。
0.142857142857142857・・・・・・・
小数で書くと、こんなにややこしい数も、
分数で書くと、とってもかんたんです。
1/7
つまり、
1/7 = 0.142857142857142857・・・・・・・
それなら、もっとややこしい
/2 = 1.41421356・・・・・・
を、小数でなくって、分数で書くとどうなるでしょう。
じつは、分数でもきっちりした分数では書けなくて、
(無限)連分数をつかって、こんなふうに書けるというお話だったのです。
1
/2 = 1 + 1
2+ 1
2+ 2+
・・・
掲載内容の無断転載、転用、編集を禁じます。(c)
小林吹代
All Rights Reserved, (c)kobayashi fukiyo , 2001